 よれば固定軸のまわりの回転においては
よれば固定軸のまわりの回転においては(慣性モーメント)×(角加速度)=力のモーメント
の次のような関係が成り立つ。
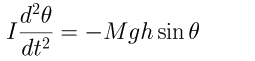 (1)
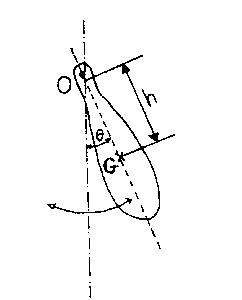
(1)ここでIは点Oのまわりの慣性モーメント
(moment of inertea),
d2θ/dt2は角速度、gは重力の加速度、hは支点
Oと重心Gとの距離である。今θが充分小さいとき
には(1)式の右辺のsinθはsinθ≒θと近似され、
(2)式で表され、その周期T0が求まる。
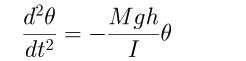 (2)
(2) (3)
(3) よれば固定軸のまわりの回転においては
よれば固定軸のまわりの回転においては
(慣性モーメント)×(角加速度)=力のモーメント
の次のような関係が成り立つ。
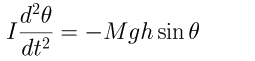 (1)
(1)
ここでIは点Oのまわりの慣性モーメント
(moment of inertea),
d2θ/dt2は角速度、gは重力の加速度、hは支点
Oと重心Gとの距離である。今θが充分小さいとき
には(1)式の右辺のsinθはsinθ≒θと近似され、
(2)式で表され、その周期T0が求まる。
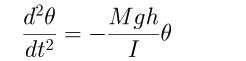 (2)
(2)
 (3)
(3)
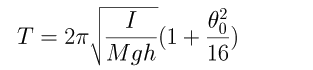 (4)
(4) (5)
(5)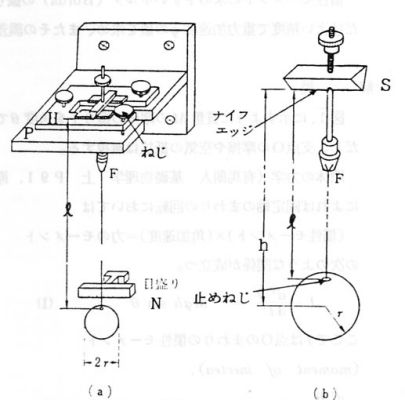 Bordaの振り子は支持具Sに細い
Bordaの振り子は支持具Sに細い
針金をつけ、反対の端に半径r、質量
Mの重い金属球をつけて鉛直につり下
げ振らせるものである。右図からわか
るように、支持具Sのナイフエッジを
支点として振動するので、式(4)のhは
、h=l+rとなる。ただしlはナイフエッ
ジから金属球の取りつけ点までの距離
である。一般に半径r、質量Mの球の
中心を通る軸のまわりの慣性モーメン
トは2/5Mr2であり、中心を通る軸に
平行でhだけ離れた軸のまわりの慣性
モーメントIとの間には
 (6)
(6)
の関係がある。(基礎物理学P95参
照)
h=l+rとして(6)を(5)に代入すると
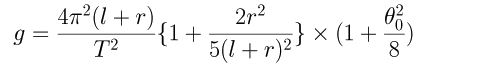 (7)
(7)