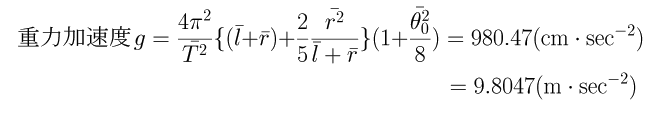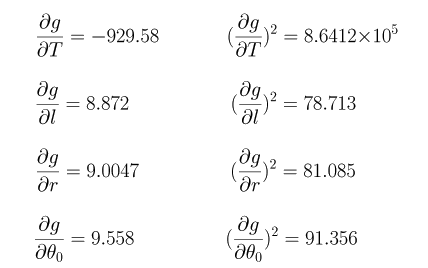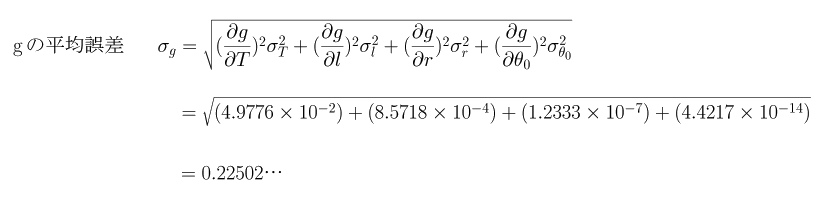(2).支持具Sの十字型チャックFの中央に長さ1mのピアノ線を入れて締め付け固定します。反対の端には金属球を固定します。
 |  |
(3).Sを水平台Hの上に置き、金属球を静かにつり下げます。
 |  |
| (4).次にナイフエッジに直角の方向に約3度(振幅で4~5cm程度)の角度で、金属球が楕円を描かないように振らせ、 10周期(10T1)を望遠鏡を用いて0.01秒の精度で測定します。望遠鏡は振り子の前方約1.8mの位置に置きます。 次に視野の中に十字線がはっきりと見えるように、接眼レンズを調節し、その十字線の中央に静止している振り子のピ アノ線の像がはっきりと見えるように望遠鏡の向きやピントを調整します。 |
 |  |  |
|
|
|
|
|
|
| 回 | d(cm) | a1(cm) | a2(cm) | θ0 | 残差 | (残差)2 |
| 1 | 106.9 | 4.5 | 4.0 | 3.968793×10-2 | 2.9564×10-4 | 8.740301×10-8 |
| 2 | 106.9 | 4.4 | 4.0 | 3.924448×10-2 | -1.4781×10-4 | 2.184780×10-8 |
| 3 | 106.9 | 4.4 | 4.0 | 3.924448×10-2 | -1.4781×10-4 | 2.184780×10-8 |
| 平均 | --- | --- | --- | 3.939229×10-2 | ∑(残差)2=1.310986×10-7 | |
| 回 | 時刻t1 min' sec |
回 | 時刻t2 min' sec |
t2-t1=100t min' sec |
t/100 sec | 残差 | (残差)2 |
| 0 | 0.0 | 100 | 3`30.97 | 3`30.97 | 2.1097 | 2×10-4 | 4×10-8 |
| 10 | 21.08 | 110 | 3`51.99 | 3`30.91 | 2.1091 | -4×10-4 | 1.6×10-7 |
| 20 | 42.19 | 120 | 4`13.05 | 3`30.86 | 2.1086 | -9×10-4 | 8.1-7 |
| 30 | 1`03.29 | 130 | 4`34.34 | 3`31.05 | 2.1105 | 1×10-3 | 1-6 |
| 40 | 1`24.36 | 140 | 4`55.30 | 3`30.94 | 2.1094 | -1×10-4 | 1-8 |
| 50 | 1`45.43 | 150 | 5`16.38 | 3`30.95 | 2.1095 | 0 | 0 |
| 60 | 2`06.64 | 160 | 5`37.52 | 3`30.88 | 2.1088 | -7×10-4 | 4.9-7 |
| 70 | 2`27.63 | 170 | 5`58.67 | 3`31.04 | 2.1104 | 9×10-4 | 8.1-7 |
| 80 | 2`48.65 | 180 | 6`19.71 | 3`31.06 | 2.1104 | 1.1×10-3 | 1.21-6 |
| 90 | 3`09.92 | 190 | 6`40.78 | 3`30.86 | 2.1086 | -9×10-4 | 8.1-7 |
| (0.01秒の桁まで測定すること) | 平均100T | 210.95s | 2.1095 | ∑(残差)2=5.34×10-6 | |||
| (6).周期測定の終わった振り子を、長さlの測定用枠(別の場所に設置してある)に吊し、ナイフエッジから 球の上部までの長さlを直角定規をあてて、視差のないように0.1mmの精度で3回測定します。次に、 ノギスを用いて球の直径2rを種々の位置で0.1mmの精度で5回測定します。 |
 |  |  |
| 回 | l(cm) | 残差 | (残差)2 |
| 1 | 108.41 | -6.666×10-3 | 4.443556×10-5 |
| 2 | 108.42 | 3.334×10-3 | 1.111556×10-5 |
| 3 | 108.42 | 3.334×10-3 | 1.111556×10-5 |
| 平均 | 108.4166 | ∑(残差)2=6.666668×10-5 | |
| 回 | 2r(cm) | r(cm) | 残差 | (残差)2 |
| 1 | 4.130 | 2.065 | -2×10-4 | 4×10-8 |
| 2 | 4.130 | 2.065 | -2×10-4 | 4×10-8 |
| 3 | 4.130 | 2.065 | -2×10-4 | 4×10-8 |
| 4 | 4.131 | 2.0655 | 3×10-4 | 9×10-8 |
| 5 | 4.131 | 2.0655 | 3×10-4 | 9×10-8 |
| 平均 | 4.130 | 2.0652 | ∑(残差)2=3.0×10-7 | |
(7).以上の測定から、物理量T、r、Dの平均値を求め、最確値とします。振れ角の最大値θ0は

であるが、空気抵抗や摩擦のために振幅は減衰しているので、振れ角の平均値θ0を

で与え、この関係から、3個のθ0を求め、平均して最確値を求めます。またπも5桁の値を用います。
| (8).前項までで求めた物理量T、l、r、D、θ0の最確値およびπの値を用いて解説の(7)式にこれらの値を入れて重力加速度gを算出します。 以下がその結果です。また表中にある残差とは測定値から平均値をひいた値で後で平均誤差を求めるときに用います。 |