基礎的な電磁気学の講義です。マックスウェル方程式までを取り扱います。高校での物理の履修と,大学1年生で習う力学の知識が必要です。教科書は,サーウェイ著『基礎物理学II. 電磁気学』東京化学同人 です。
2023 年度は、オンラインでの講義となりました。上の写真は撮影した教室です。以下に、2 回目以降の録画映像をあげます。1 回目は、課題の回答方法の練習等でしたので省略します。
- 2 回目
クーロンの法則の実験映像は「メディア教育開発センター」制作のもの - 3 回目
- 4 回目
- 5 回目
- 6 回目
- 7 回目
- 8 回目
- 9 回目
- 10 回目
- 11 回目
- 12 回目
- 13 回目
- 14 回目
- 15 回目
後日、また追加します。
以下、講義中のデモと内容はおなじですが、短めに作成した動画をあげて、またその解説を書いてみます。
(電荷の性質:電気力)
電気的な現象としては,まず最初に電気的力があげられると思います。下の動画では,ガラス棒を絹布で摩擦して,導体や絶縁体との間の力を見てみました。導体と絶縁体は絹糸で吊るされています。
導体も絶縁体も,最初は引き寄せられます。導体の方はガラス棒に接触すると,すぐさま反発して離れます。絶縁体は接触からしばらく時間をおいて離れます。離れた後は,どちらもガラス棒との間に反発力が働いているように見えます。
(電荷の性質:正と負の1)
電荷には 2 種類あるとして,フランクリンが正電荷,負電荷と名付けました。ガラスの棒を絹でこするとガラスの棒が正に帯電し,エボナイトを毛皮でこすると負に帯電するのですが,この電荷の種類の違いを観測してみます。観測には微弱な電流を検知する検流計を使用します。検流計が右に振れるのか,左に振れるのかで性質の異なる電荷があることを観測してみます。
ただし帯電したガラス棒で検流計に直接触れても針はほとんど振れません。ガラスは導体ではないので,帯電していてもその電荷が移動しにくいのです。そこで箔検電器を使って,電荷をいったんそこに移します。
上の状態では,ガラス棒の近くに負電荷が集まり,下の箔のところに正電荷があると考えられます。ここで箔検電器に手で触れてみます。
上の写真のように,箔が閉じます。これは下方に在った正電荷が手を通じて外へ流れ出してしまったからなのですが,この後手を離した後ガラス棒を離すと,箔検電器には負の電荷だけが残ります。
全体に,負の電荷が行き渡るので箔は再び開きます。このようにして,最初の電荷の符号とは反対になりますが,電荷を箔検電器に移すことができました。
ガラス棒とエボナイトで同じように電荷を箔検電器に移して,検流計の振れる方向を観測しました。
確かに,反対方向に針が振れました。よって,電荷には 2 種類あることが推測されます。検流計の一端は接地されています。
ただ,検流計ではなくもう少しシンプルな方法でやらないと,検流計がブラックボックスで,そちらの方が謎が深いです。
(電荷の性質:正と負の2)
よく教科書などに載っているセロテープを使った実験をやってみました。最初はテープ2枚を机の異なるところに張り付けて引きはがすものです。
反発力が働いています。次にテープを重ねて張って,机から一緒に引きはがしたのち,二つに分けるものです。
引力を生じていることが見て取れます。
(絶縁体と導体)
電荷には伝導性がありますが,これは1792 年にイギリスのグレーによる実験で,はっきりと示されました(参考文献:『電気の歴史』高木純一,昭和42年,オーム社)。グレーはガラス管を使った電気の実験をしていたのですが,ガラス管内に塵が入り込むことからコルクで栓をしました。そうすると今度はコルクに塵が引きつけられます。彼は電気がコルクに移動したと考えて,これがどこまで移動するものか確かめる実験を試みました。途中途中をひもで吊り下げて針金を水平に張って,最終的には\(100 \, \mathrm{m}\) の距離まで試しています。この実験では,最初電気は伝わらなかったのですが,吊り下げる糸を絹に代えると電気が伝わることを観測しています。このような観測から電気を伝える材質と伝えない絹のような材質があるという観念が確立してきます。
グレーと同じ実験を試みます。エボナイトに生じた電気を針金を通じて箔検電器で観測します。
左方に金属の円盤が釣られていて針金とクリップで固定されています。針金は絹糸で吊るされていて,右端は箔検電器に接続されています。
エボナイトを擦って左側の円盤に近づけてみました。
念のために箔検電器を針金から切り離して同じことをやってみました。多少針金の途中で放電しているように思えます。直接箔検電器にエボナイト棒を近づける場合よりも箔の開きが小さいですね。授業中にやるときには,針金をまっすぐに伸ばしもっと距離を離して試みてみます。
(静電誘導)
金属に帯電した物体を近づけると,自由電子が移動して帯電体に近いところは帯電体の電荷と反対符号の電荷が多くなり,遠いところは同符号の電荷が多くなります。このような現象を静電誘導といいます。以下の実験では,このときの電荷の移動を検流計を使ってみて見ます。
二つの金属板を絹糸で吊るして,検流計を間に挟むようにして導線で繋ぎます。帯電したエボナイトの棒を金属板に近づけて電荷の移動が検出できるか試みます。
フルスクリーンぐらいじゃないと分かりにくいです。導線をはずした場合もやってみましたが,確かに違いは見て取れるので,導線を電荷が移動しているのだろうと推測されます。
(静電遮蔽)
導体で囲まれた空間は,外部の電場の影響を受けません。導体で囲みその導体を接地して,外部の電場の影響を遮断することを静電遮蔽といいます。
上の写真では,エボナイトは帯電しているのですが,箔検電器の上を金網で覆うと箔は開きません。金網で電場の影響が断ち切られています。全体を覆うのではなく部分的に覆うだけでも十分な効果が現れています。ただし,手で金網に触れていることもポイントで,これを金網の柄の部分に持ちかえると,下の写真のように箔が開きます。
このときの動画です。
(静電遮蔽その2)
バンデグラーフ起電機を使って,導体内部に電界が無いことを観察してみます。

上の写真の手前にある缶にはアルミの蒸着膜が周りと内側に貼り付けられています。バンデグラーフを動かして,放電さで缶と繋いで見ます。
缶の真上の方から見てみました。
内側の箔は立っていません。
このときの動画です。三つほど撮影しました。
缶の真上の方からの撮影です。
缶の中に放電さを差し込んでみました。
缶の中に放電さを挿入すると缶の内側も外側も箔が立っています。
(導体の内部には電荷が存在しない)
導体の内部には(余分な)電荷がありません(電気的に中性と言った方が正確です)。先ほどのアルミ膜を貼り付けた導体の缶を使って,このことを確かめてみましょう。たくさんの電荷が必要なのでバンデグラーフで起こした電気を利用しますが,バンデグラーフはあまりにも周囲に電荷をまき散らすので,いったんそれをライデン瓶に蓄えて利用してみます。
ライデン瓶に電荷を蓄えて,その電荷を放電さで写真中央の導体の缶に移します。その後で,写真の奥の方にある発泡スチロールの棒の先にアルミ箔を巻いたものを使って電荷の有無を調べます。まずは棒を缶の外側に接触させ,そこに電荷があるかどうか箔検電器でみてみます。その後同じように,缶の内側も調べてみます。
確かに内側と外側では箔検電器の反応が異なりました。外側に電荷があるのは,箔検電器で試さなくてもアルミ膜の立ち具合を見て明らかです。それに比べて内側は箔検電器によると,ほとんど電荷がなさそうです。この実験は非常に難しいところがあって,箔検電器に電荷を移すときに絶縁がしっかりした棒を使わないと自分自身の体を通じて電荷が失われてしまいます。それゆえ発泡スチロールの棒を使用していますが,これが身近にあるもので最も絶縁性が良いものでした。ライデン瓶を運ぶときや,導体缶から電荷をもらうとき等で,絶縁をきちんとしていないと自分の体を通じて電荷が流れ出してしまいます。
(オレンジジュースの電池)
オレンジジュースと2種の金属(銅と亜鉛)を使って電池を作ってみます。紙コップを加工して,内側に銅板と亜鉛板を貼り付けます。
まず,電圧を測ってみます。針式の電圧計と繋ぎます。
オレンジジュースをコップに入れてみました。電圧計のレンジは 1V です。
0.66V ぐらいでしょうか。もう一つ電池を使って,直列に繋いで見ます。
動画を撮りました。針が振り切れたのでレンジを 3V に変更しました。
直列だと 1.3V ぐらいです。だいたい2倍になっています。
電流を測ってみます。念のため 10 Ω の抵抗を繋ぎます。奥にあるでかいのが抵抗器です。ダイヤルで抵抗値を設定できます。10 Ω に設定しました。
一個の場合と直列の場合を測定しました。測定金レンジは 300 μA です。測定の動画です。
電流値が安定しません。また電圧測定と違って,直列にした場合に電流値は 2 倍になっていないようです。電流値の大きさからいっても,かなり電池の内部抵抗が大きいようです。
デジボルの方が電圧を正確に測れるというので,測定器を変更してみました。下記は電池 1 個の測定です。
針式の電圧計で測った場合より大きめの電圧になっています。
電池一個の場合と直列の場合の電圧をを測定しました。その動画です。
電圧は安定しています。直列にすると電圧はほぼ 2 倍になっています。
(エルステッズとアンペールの実験・電流の磁気作用など)
エルステッズが発見した電流の磁気作用の実験です。ボルタの電池の発明から20年後ぐらいに見つかっています。
一本の銅線ではなくて,何重かになったものですが,これに電流を流して方位磁針の振れを見てみます。
ゆっくりと電流を増やしています。最大で 0.4 A 程度です。地球磁場と平行になるように電流を流しています。ある程度の角度磁針が振れているので,地球磁場と同程度の磁場を電流が作り出していると予想されます。
アンペールの実験の方をやってみます。島津の装置です。
二つの四角い電流ループがあって一辺を近接して置きます。近接した辺の長さは 40 cm で,右側のループは 10 巻きです。この電流間の力を検出するわけですが,左側はヤジロベーになっていて右側は何重かになっています。両方共通の電流が流れるように配線してあります。ヤジロベーの調節が難しくて十分でないのか 0.4 A 程度では,ほぼ反応しない。それで 1.5 A 程度流してみました。実験の動画です。
大きく写さないと変化が分からないのでアップにしました。ピッという音とともに電流を流して(電源のスイッチの音です),その後切っています。反応が見えないことはないのですが,これぐらいだと学生に大したことないと思われそうです。
電流間に生じる力ではなくて,電流が磁場から受ける力を観察してみました。
永久磁石のつくる磁場に電流を通してみます。アルミの箱の上に載っているのが磁石です。観測の動画です。
こちらは大きな反応がありました。電流の一部しか磁場中にないのですが,電流間の力とは大きさがかなり異なるようです。
どのぐらいの磁場が生じているのか測ってみました。
上の写真の左側にあるのが磁場の測定器です。白い筒の先端にセンサーがあります。電流が 0.4 A 程度では,ほとんど検出されません。このレンジ用の測定器ではないのですが, 1.5 A 程度にまで電流を増やして測定しました。測定の動画です。
音が小さいのですが,「ピ」という音とともに電流を流し始めています。最初は 1 cm あるか無いかぐらいの距離で, 0.3 mT 程度増加しています。その後でセンサーを少し離してみました。数センチ放すとほとんど観測されません。先のマグネットも測定しました。
こちらは桁違いに磁場が大きいです。 3 mT 程度でしょうか。
(電流が磁場から受ける力)
\(F = I \, B \, L\) の実験です。これは何の法則というのか分かりません。アンペールの法則ではないですね。
上の写真に使用する物が並んでいます。コイルが作る磁場の中に電流を置いて,その電流が受ける力を測定します。コイルの中に差し込まれているのは,下記のプリント回路です。短い辺の長さは 2.6 cm です。1/2 や 2/3 の位置に印が入っています。
差し込んだところはこんな感じです(下図)。ただ置いただけですが釣り合っていて,ゆらゆら揺れています。プリント基板の短い方の辺が磁場から力を受けます。プリント基板とコイルに同じ電流が流れるように配線しました。小さな抵抗として 0.1 Ω の標準抵抗を挿入しています。
釣り合いの位置を見る為に,グラフ用紙を使います。
電流を流したときに,プリント基板のコイルの外にある部分が持ち上がるように電流を流します。その力を測るためにプリント基板に細い銅線を載せます(下図)。実際は銅線を先に載せて,釣り合うように電流の大きさを調整します。
実験の様子です。最初は電流を流していませんし,おもりも載せていません。このときに揺れている位置を記憶しといてください。おもりを載せた後で電流を増加させます。
1.2 A 程度で元の釣り合いの位置に戻ったようです。銅線は 10 cm で,質量は\(10.5 \times 10^{-6} \, \mathrm{kg}\) です。コイルの作る磁場は,コイル定数が \(B / I = 3.68 \times 10^{-3} \, \mathrm{N/A^2 m}\) なので,\(4.4 \times 10^{-3} \, \mathrm{T}\)です。
(クルックス管)
クルックス管のデモなのですが,教室で実施できるかどうか心配です。かなり暗くないと陰極線が見えません。
丸い加速用の電極と,熱電子放出用のヒーター,偏向電極があります(下図)。ヒーターは加速用電極の左側の中に半分隠れています。加速用の電極は中心に穴があいています。
部屋の明かりを消して,クルックス管用の電源のスイッチを入れました。このときにヒーターが赤く灯ります。その後,電子を加速する電極に電圧を加えたら陰極線が放出されます。加える電圧は固定電圧で, 300 V です。下がその動画です。
偏向極板に電圧を加えてみます。下の写真は極板のところのアップです。
上向きに偏向させる場合と下向きに偏向させる場合の両方をやっています。
少しひいた映像も撮影しました。
コイルで磁場を加えてみます。
コイルの中心に置いていないのですが,見逃してください。右にあるのがコイルに電流を流す電源です。ゆっくりと電流を増加させてみました。下がそのときの動画です。陰極線がだんだん下方にずれていきます。
横からの映像の方が良かったか?それは後で考えます。1 A 流したときの磁場を測定してみました(下の写真)。電流を流す前が N 0.4 mT で,流した後が S 0.3 mT なので,0.7 mT 程度の磁場です。
磁場と平行に陰極線を入射させてみました。下の写真のようにコイルの中に差し込みます。
ゆっくりと磁場を加えていくと,陰極線が螺旋を巻き始めます。下がそのときの動画です。
別な角度から撮影しました。
最後に,螺旋の写真を2枚ほど。
以前,作成した陰極線のページです。
(追加)磁場を加えて偏向させる場合を真横から取り直してみました。電流値が見えませんが,最大で 1 A 流しています。
もう一つ,磁石を近づけた場合の様子を撮影しました。
あと,静止画を数枚あげときます。
(ファラデーの誘導起電力)
ファラデーの誘導起電力の実験です。下に使用する機材をあげます。
ファラデーの最初の試みは鉄の輪にコイルを二つ巻き付けてその片方に電流を流すというものでした。ファラデーは,近接して置かれた導線の回路の片方に電流を流して,もう片方に影響がないのは,静電誘導の場合と比較して非常に不思議なことだと考えたようです。静電場ならば片方が電荷を帯びるとき,必ずもう片方の導体に影響がでますから。いろいろ試みているうちに変化が重要だと気づきます。
上の写真では単に二つのコイルを近くに置いただけです。右側のコイルに電流を流します。左側のコイルには検流計が繋がれています。下が実験の動画です。コイルの間の距離を離した場合も観測してみました。
コイル間の距離以外はほぼ同じ条件なので,二つのコイルの間の結びつきの影響が見て取れます。
ファラデーは二つのコイルを同じ鉄の輪に巻いたのですが,ここでも二つのコイルの間を鉄製のモンキーレンチでつないでみます。モンキーがない場合とある場合を比べてみました。下がその動画です。
多少影響が見て取れます。
ファイラデーは最終的に電流を利用せずに磁場だけで電気を得ることに成功します。以下でも磁石のみで電気を得てみます。丸い磁石を使用します。これは確かスピーカー用のものだったような?
コイルと磁石の相対的な位置を変化させるだけで,電気が得られます。下がその動画です。
継続的に電気を起こそうとすると,磁場を際限なく増加させることはできないので,磁場の増減を繰り返すことになります。回転運動などを利用して周期的に磁場を増減させます。教科書では良くコイルを回転させてますが,以下では磁石を回転させてみます。
二つのコイルを導線で繋ぎました。その間で磁石を回転させます。磁石はコイルが作る磁場と似たような磁場を作るタイプで,片面が S 極で,もう片面が N 極です。下の動画がそのときのものです。
電流の時間変化が激しいためか,片側に針がずれていますが配置的には左右均等に針は振れそうなものです。しかし,磁石の回転が遅くなると左右対称に近くなってきているように思えます。今度はオシロスコープを使って,電圧を見てみましょう。
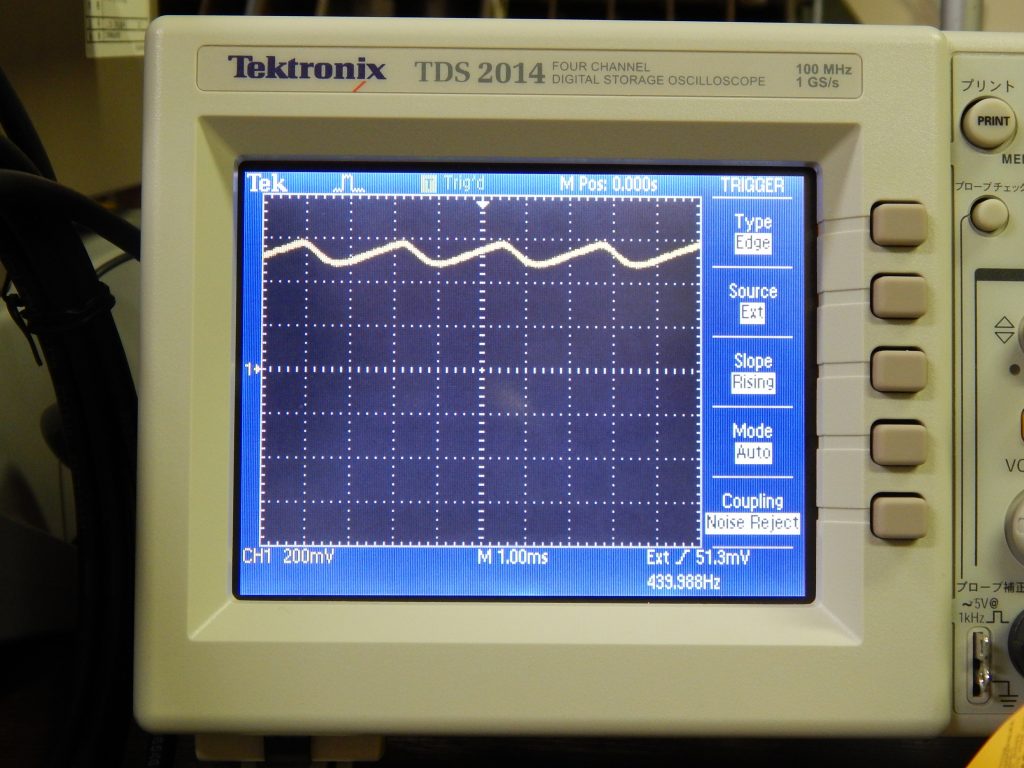
なぜかノイズが多かったので,コイルを片方だけにしました。下がその動画です。
このつなぎ方では,コイルに電流は流れていないはず(先の場合と条件が異なるかもしれません)。なぜか3角波の波形です。磁石の回転が遅くなると振幅が小さくなっているので起電力を観測できているのではないでしょうか。
(交流回路でのコイル)
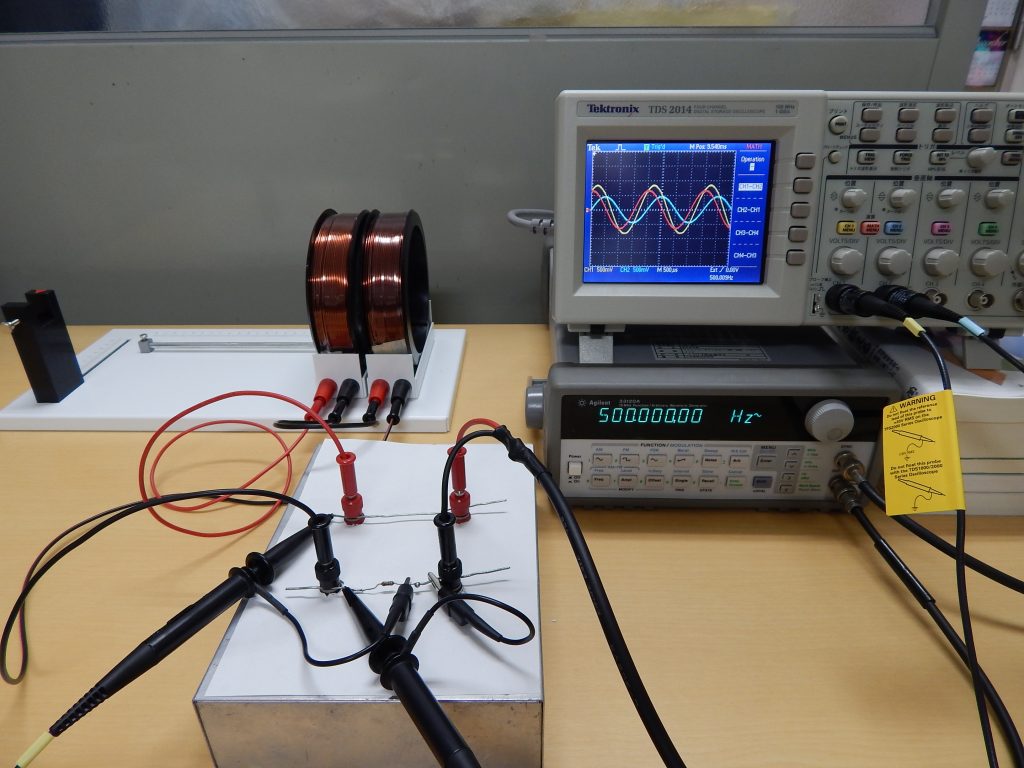
交流回路では,コイルとキャパシターの振る舞いが直流の場合と大きく異なります。交流発信器とオシロスコープを用いて,その違いを観てみます。下の写真で箱の上に在るものは,\( 10 \, \mathrm{\Omega}\) の金属被膜抵抗です。発信器で 500 Hz の交流を抵抗に流して,抵抗の電圧をオシロスコープで観測しています。
オシロスコープの画面状の青いラインはオシロスコープの ch 2 に入力された電圧を示しています。
まず最初に,抵抗に方形波を加えます。その後で,回路にコイルを加えてみます。コイルは電流の変化を妨げる働きをするので,方形波の四角い波形がどう変化するのか観測します。最後に,コイルを 2 個つないでみます。下が観測の動画です。
下に,最後の状態の写真をあげます。コイルをつなぐことで,抵抗の電圧,すなわち回路に流れる電流の変化が緩やかになっています。オシロスコープの横の目盛りは \(100 \, \mathrm{\mu s}\) です。コイルを 2 個つなぐと更に変化がゆっくりになりました。
続いて,コイルに加わる電圧を観測してみます。コイルは回路の途中に位置しているので浮動電位の測定方法で測ります。ch 1 と ch 2 の 2 つのプローブで挟み込む様にして,ch 1 の電圧から ch 2 の電圧を差し引きます。プローブの負極は発信器の負極に両方ともつなぎます。ch 1 の電圧は黄色の線で, 引き算した電圧は赤線で表示されます。このように演算をするときには,それぞれのチャンネルの縦のスケールを合わせる必要があります。
最後の状態の写真を下記にあげます。コイルの電圧(黄色)の方が大きくて,抵抗の電圧(青)を差し引いても,黄色と赤でそれほど変化は無いのですが,一応赤がコイルのみの電圧です。コイルに加わる電圧は電流の時間微分に比例しますが,それらしい形には成っています。ただし,黄色の電圧は本当は方形波になるべきではないかと考えると . . .
次に,コイルの電圧の位相を観てみます。発信器の出力を方形波から正弦波に変更して,位相を観測します。下記に測定の動画をあげますが,入力を正弦波に変更したあと,横軸と縦軸を調整しています。回路に流れる電流(青線)の位相が表示の中央にくるようにしました。一周期はマス目4個分です。
最後の状態の写真を下記にあげます。コイルに加わる電圧(赤線)はマス目一個分だけ左にずれています。位相でいえば \( \displaystyle \frac{\pi}{2} \) 位相が進んでいます。表示は横軸が時間軸なので,赤の信号の方が先にピークを迎えていて,青の信号がピークとなるのは赤よりも遅れています。波動の位相を考える場合,X – Y 座標のグラフでは,(右方へ進む波の場合)ピークが右にある方が位相が進んでいるのですが,横軸が時間の場合にはピークが左にある方が位相が進んでいます。
(整流回路)
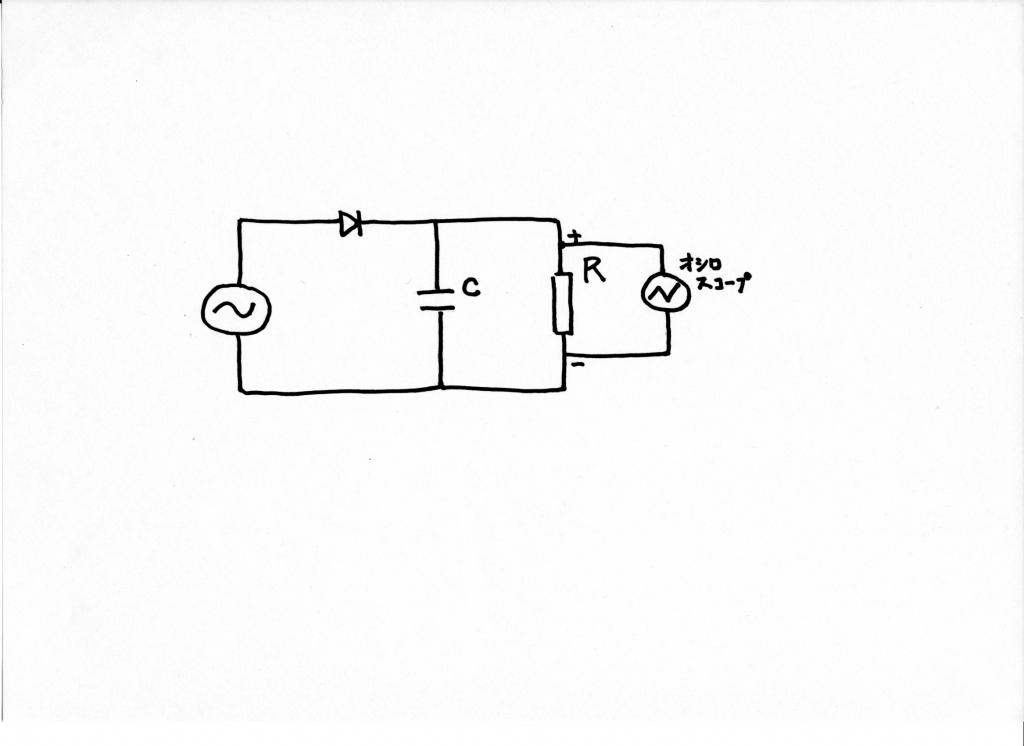
キャパシターは電荷を蓄えるものですが,その機能を利用する例として交流から直流を生成する整流回路を取り上げます。と言っても簡単な例ですが。
上の写真では発信器に \(1.4 \, \mathrm{k \Omega}\) の負荷をつないで,その両端の電圧をオシロスコープに表示しています。まずはダイオードを用いて交流の一方向の流れのみを取り出します。発光ダイオードなので,発信器の周波数を下げてダイオードの点滅を見てみました。下に観測の動画をあげます。
10 Hz のときの写真を下記にあげます。
電圧の正の側と負の側が対称的ではありません。ダイオードに加わる電圧が \(1 \, \mathrm{V}\) 程度を越えたあたりから電流がダイオードを通っているようです。それで発信器の電圧を上げて通過する電流を増やしました。
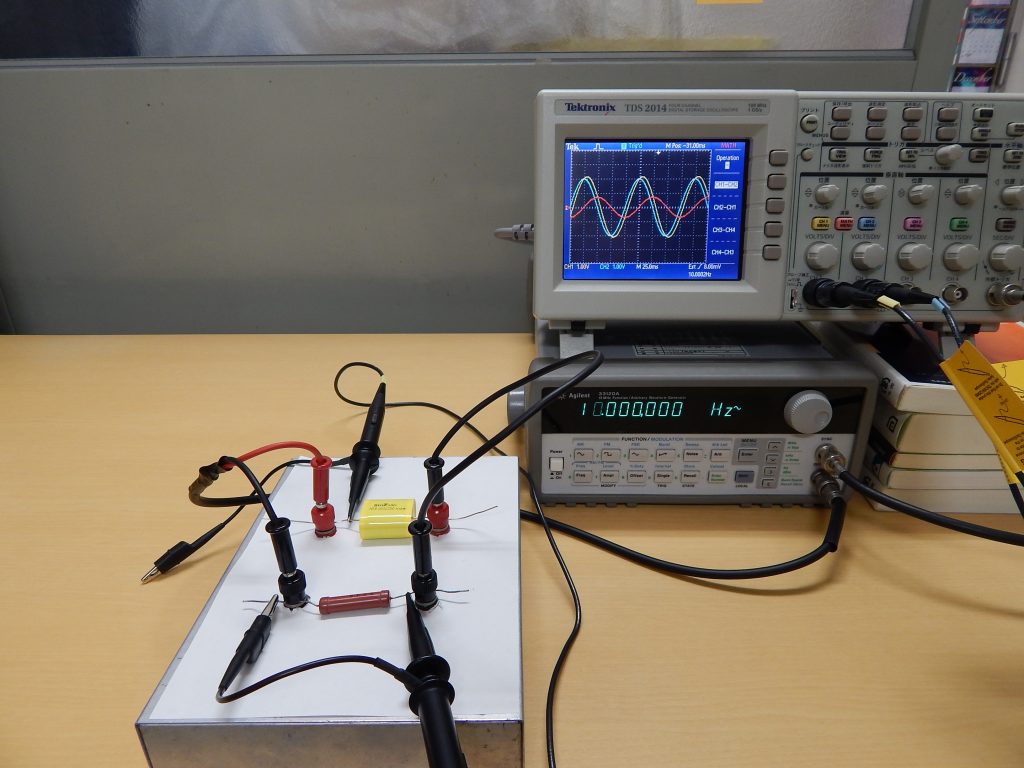
発信器の周波数を \(60 \, \mathrm{Hz}\) に上げた後,負荷と平行にキャパシターをつなぎます。下にそのときの動画を上げます。脈打ってますが,正電圧のみが負荷に加わっていることが分かります。発信器の周波数を下げて,整流された電圧の違いを観てみました。
最後の状態の写真を下にあげます。
\(60 \, \mathrm{Hz}\) だと,ある程度の正電圧が保たれているのですが, \(5 \, \mathrm{Hz}\) では,キャパシターからの放電電流が枯渇して最後の方では負荷に加わる電圧がほぼゼロになっています。
回路図を下記にあげます。
(交流回路でのキャパシター)
キャパシターに加わる電圧は蓄えられている電荷で決まります。つまり回路に流れた電流の蓄積に比例しますが,それは電流の時間積分ということになります。コイルに加わる電圧が電流の時間微分に比例するのとは対照的です。以下ではキャパシターの電圧の時間変化をみてみます。

上の写真のようにキャパシターと抵抗を直列につなぎます。キャパシターをプローブ1(黄色)とプローブ2(青)で挟み込んで,その電圧の差をとってキャパシターに加わる電圧を観測します。以下がその動画です。
最後の状態の写真を下記にあげます。
抵抗に加わる電圧は青色の線ですが,動画の最後の方で青の線のピークをオシロの画面の中央に合わせました。1周期は4マス分でキャパシターの電圧を示す赤の線が一マス右にずれていて,4分の1周期遅れてピークを迎えています。
下に,方形波を入力したときの写真をあげます。この解釈は難しいですね。
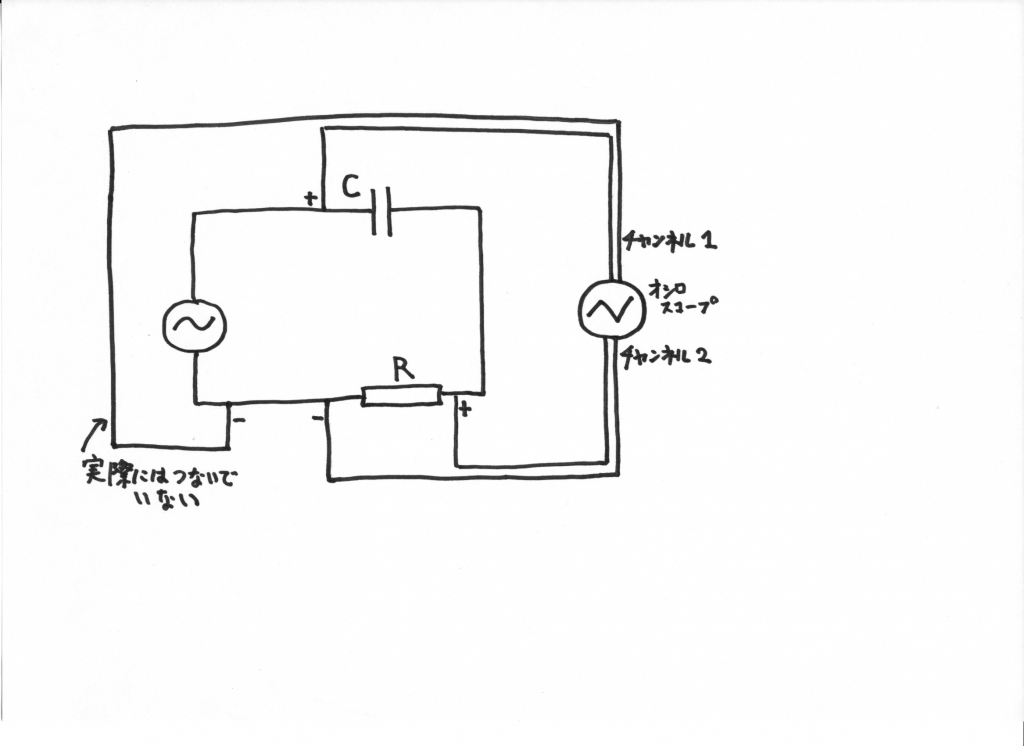
オシロのつなぎ方などの図を下にあげます。
(交流回路でのキルヒホッフの法則)
交流回路でのキルヒホッフの法則を観てみます。
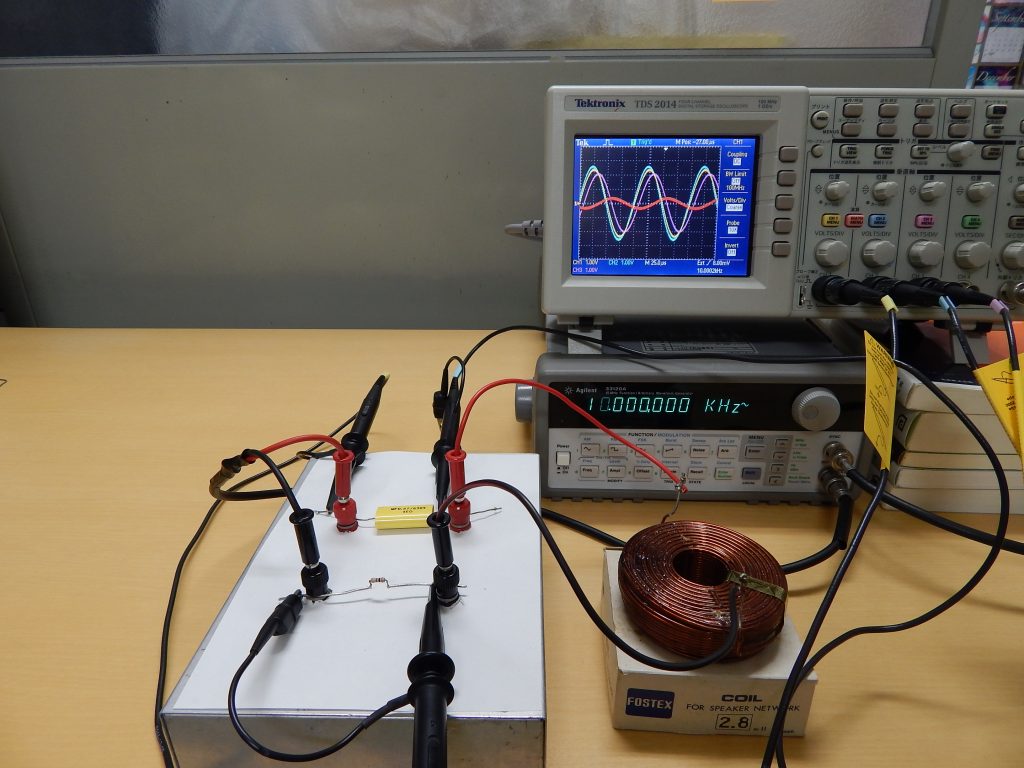
上の写真にあるように,コイルとキャパシターと抵抗を直列につなぎます。プローブを3本使います。オシロの画面の紫の線がプローブ3で抵抗に加わる電圧を測定していて回路に流れる電流の位相を示します。最初にコイルをプローブ1(黄色)とプローブ2(青)挟み込むようにして,その差の電圧(赤)を計算してコイルの電圧を観測します。
最後の状態の写真をあげます。
コイルの電圧(赤)は \(1.5 \, \mathrm{V}\) です。抵抗(紫)の電圧は \(2.0 \, \mathrm{V}\) です。次に,キャパシターの電圧を測ってみます。プローブ1とプローブ2をキャパシターを挟み込む様につなぎ替えます。
最後の状態の写真を下記にあげます。
キャパシターの電圧(赤)は小さいのですが, \(0.35 \, \mathrm{V}\) と読み取れます。続いて,回路全体の電圧(黄色)を読み取ります。黄色の信号を画面の中央に移動させて読み取りました。
最後の状態の写真を下記にあげます。
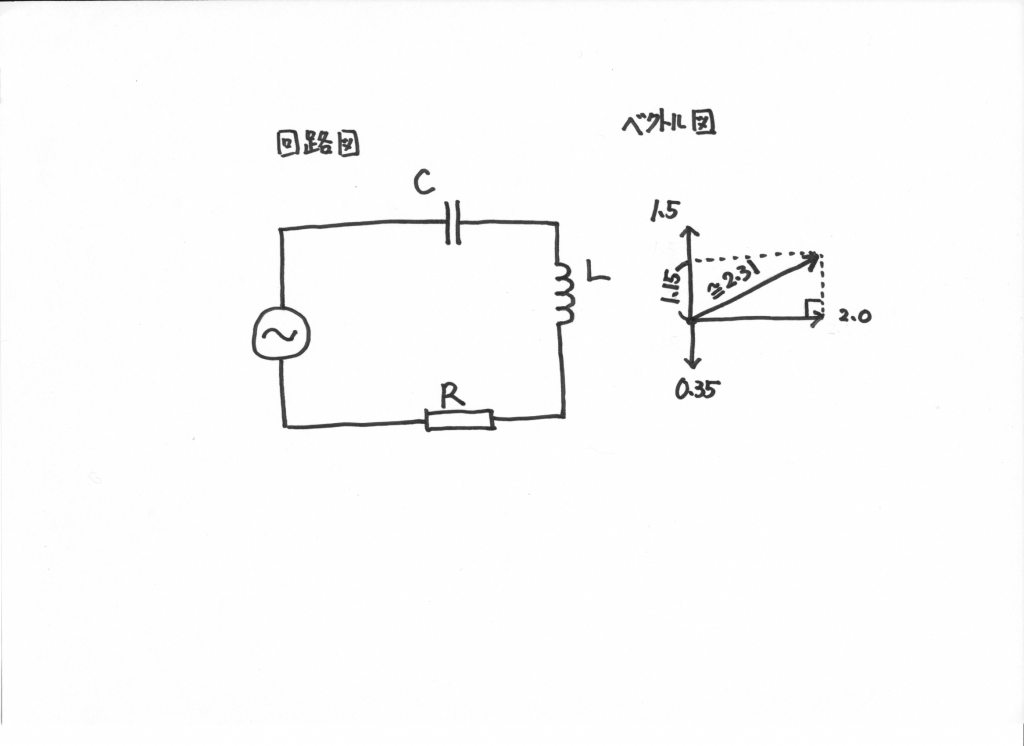
黄色の電圧は \(2.3 \, \mathrm{V}\) と読み取れます。コイルの電圧とキャパシターの電圧を引き算すると \(1.15 \, \mathrm{V}\) で,抵抗の電圧と 3 平方の定理を用いて合成して, \(\sqrt{1.15^2 + 2.0^2} \approx 2.31 \, \mathrm{V}\) となって,観測した全体の電圧 \(2.3 \, \mathrm{V}\) とほぼ一致しています。
回路図とベクトル図を下記にあげます。
(交流回路の共振現象)
交流では,コイルに加わる電圧とキャパシターに加わる電圧は位相が 180 度異なります。そのため特定の周波数でこの電圧が打ち消しあって共振と言われる現象が生じます。
上の写真にあるように,キャパシターとコイルと抵抗を直列に接続します。プローブ1(黄色)とプローブ2(青)でキャパシターを挟み込むようにして,その電圧の引き算(赤)からキャパシターに加わる電圧を測定します。発信器の周波数を 1 kHz から増加させて電圧の変化を観てみます。下がその動画です。
最後の状態の写真を下記にあげます。
周波数を上げていくと,キャパシターに加わる電圧が小さくなっています。キャパシターのリアクタンスが \(\displaystyle \frac{1}{\omega \, C} \) で,周波数が大きくなるとリアクタンスが小さくなる為です。
次に,コイルの電圧を観測します。コイルを挟み込むようにプローブを付け替えます。
最後の状態の写真を下にあげます。
今度は,発信器の周波数を大きくすると,コイルに加わる電圧(赤)が大きくなります。これはコイルのリアクタンスが \(\omega \, L\) で,周波数が大きくなるとリアクタンスが大きくなるからです。
続いて,キャパシターとコイルの電圧の和(赤)を観測してみます。キャパシターとコイルを挟み込むようにプローブを付け替えます。下がその動画です。
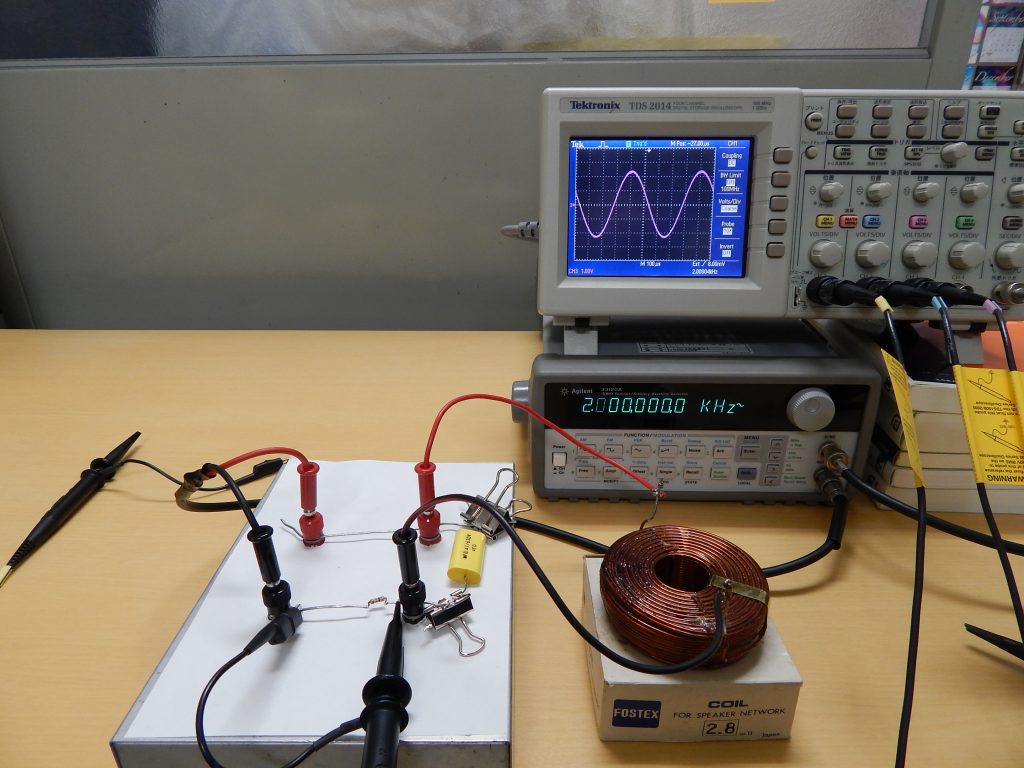
発信器の周波数が \(4.5 \, \mathrm{k Hz}\) のときの状態を下に示します。
キャパシターの電圧は周波数とともに小さくなり,コイルの電圧は周波数とともに大きくなるので,どこかの周波数で同じ大きさになるのですが,ちょうど \(4.5 \, \mathrm{k Hz}\) のあたりで同じ大きさとなって打ち消し合い,その和が最小(ほぼゼロ)となっています。これを共振現象と言います。共振の周波数は \(\displaystyle \frac{1}{2 \, \pi \, \sqrt{L \, C}}\) です。コイルのインダクタンスが \(2.8 \, \mathrm{m H}\) でキャパシターの容量が \(0.47 \, \mathrm{\mu F}\) なので,共振周波数はおおよそ \(4.4 \, \mathrm{k Hz}\) あたりと予想されます。共振状態では,回路の抵抗値が最小となるので回路に流れる電流は最大となります。
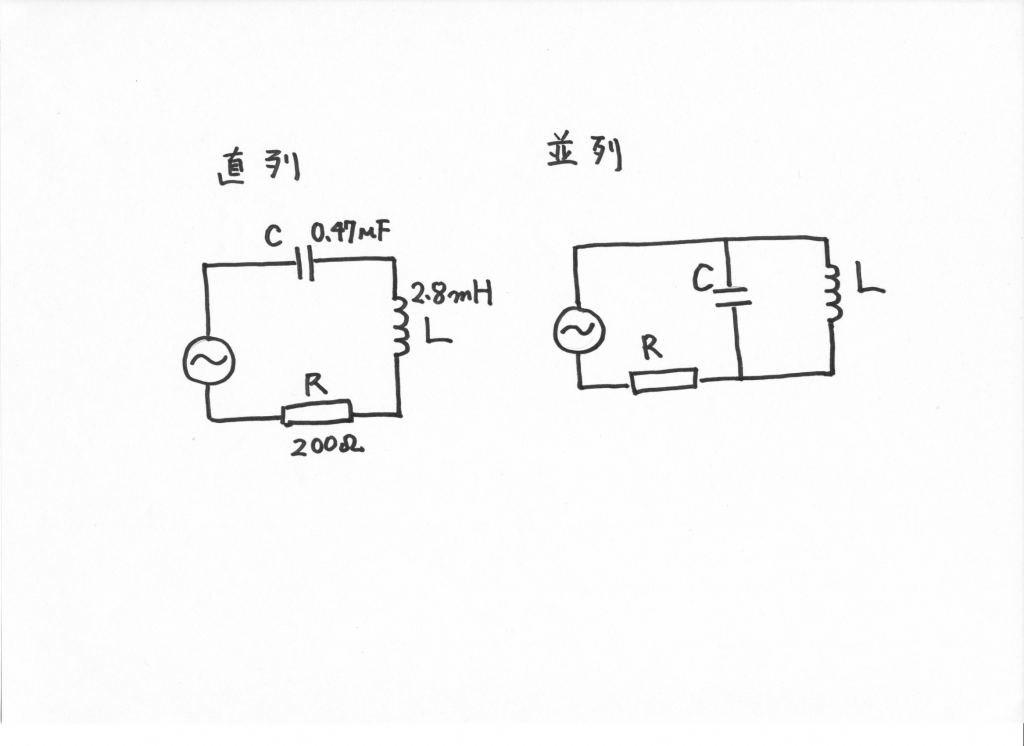
上記は,直列にキャパシターとコイルが並んでいたのですが,次は下の写真のように平行に並べてみます。
発信器の周波数を増加させながら,キャパシターとコイルの並列部分に加わる電圧を観測しました。下がその動画です。赤が並列部の電圧で,紫は抵抗の電圧です。
発信器の周波数が \(4.5 \, \mathrm{k Hz}\) のときの状態を下に示します。
発信器の周波数が \(4.5 \, \mathrm{k Hz}\) のとき,並列部(赤)の電圧は最大になっています。並列部のインピーダンスが最大となるからなのですが,それゆえ回路に流れる電流(紫)は最小となっています。この現象を並列共振といいます。
直列と並列の回路図を下記にあげます。
(波動方程式)
講義の最後が電磁波の話なのですが,波動方程式に関して予習をしてから電磁波に入りたいと考えています。
波を表す式は,それが一次元なら,変位を \(y\) として下記の式で表されます。
\[
\displaystyle y(x, t) = f(x \pm v \, t).
\]
上記は波が同じ形で進行していくことを表す式です。我々が波と言ったときに考える周期性は,この式には含まれていません(あからさまには見えないというべきでしょうか)。
電磁波を予言したマックスウェルは,もちろん波形を確認したわけではなく,波動が生じうる条件を確認しました。それは,上記の変数を用いれば,下記の式が成立することです。
\[
\displaystyle \frac{\partial^2 y}{\partial x^2} = \frac{1}{v^2} \, \frac{\partial^2 y}{\partial t^2}
\]
これを波動方程式と言います。マックスウェルは電場 \(E\) や磁場 \(B\) に関して,上記の式が成立することを発見しました。
力学的に波動現象の具体的な事例を考察すれば,その運動方程式から上記の式に相当する微分方程式が導かれます(参考サイト)。ただ,波が形を変えずに進行していくことは,物理と切り離して取り扱うことができるように思えます。以下,簡単なもので正しいかどうかも定かではないのですが,形を変えないという条件のみから波動方程式を導いてみます。
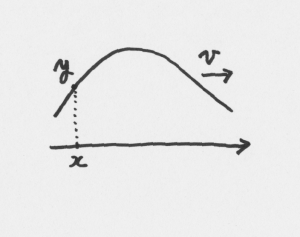
上の図のように,右へ進む波を考えます。座標 \(x\) の位置では,波が進むことで \(y\) は下がります。\(\Delta t\) 経過したとして,\(y\) の変化を \(\Delta y\) とし,波が同じ形を保つことから以下の式が成立します。
\[
\displaystyle \Delta y = – \frac{\partial y}{\partial x} \, v \, \Delta t
\]
上記から,極限を考えて
\[
\displaystyle \frac{\partial y}{\partial t} = – v \, \frac{\partial y}{\partial x}.
\]
この式は \(\displaystyle y = f(x – v \, t)\) には当てはまるのですが,左に進行する \(\displaystyle y = f(x + v \, t)\) には当てはまりません。左に進行する場合は下記の式となります。
\[
\displaystyle \frac{\partial y}{\partial t} = v \, \frac{\partial y}{\partial x}.
\]
このままだと,2つの式を場合場合で使い分けないといけません。それはちょっと…
波の形が変化しないということは,その傾きも変化しないということだと思います。
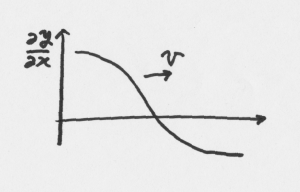
波の進行によって形を変えないという条件を使うと,右に進む波の場合,
\[
\displaystyle \Delta \left( \frac{\partial y}{\partial x} \right) = – \frac{\partial^2 y}{\partial x^2} \, v \, \Delta t
\]
先ほどの式 \(\frac{\partial y}{\partial t} = – v \, \frac{\partial y}{\partial x}\) を使って,左辺を書き代えます。
\[
\begin{align}
\Delta \left( – \frac{1}{v} \, \frac{\partial y}{\partial t} \right) &= – \frac{\partial^2 y}{\partial x^2} \, v \, \Delta t \\
\frac{\Delta \left(\frac{\partial y}{\partial t} \right)}{\Delta t } &= v^2 \, \frac{\partial^2 y}{\partial x^2}\\
\end{align}
\]
左辺の極限をとって,下記のように変形して良いのではないかと?思います。
\[
\frac{\partial^2 y}{\partial t^2 } = v^2 \, \frac{\partial^2 y}{\partial x^2}
\]
上記の式は,左へ進む波の場合も同じ式になります。変数変換をする意味は何かとか,判然としない所もあるのですが,講義では運動方程式を使った説明と,この説明の両方をしようかと思っています。
(一石トランジスタラジオ)
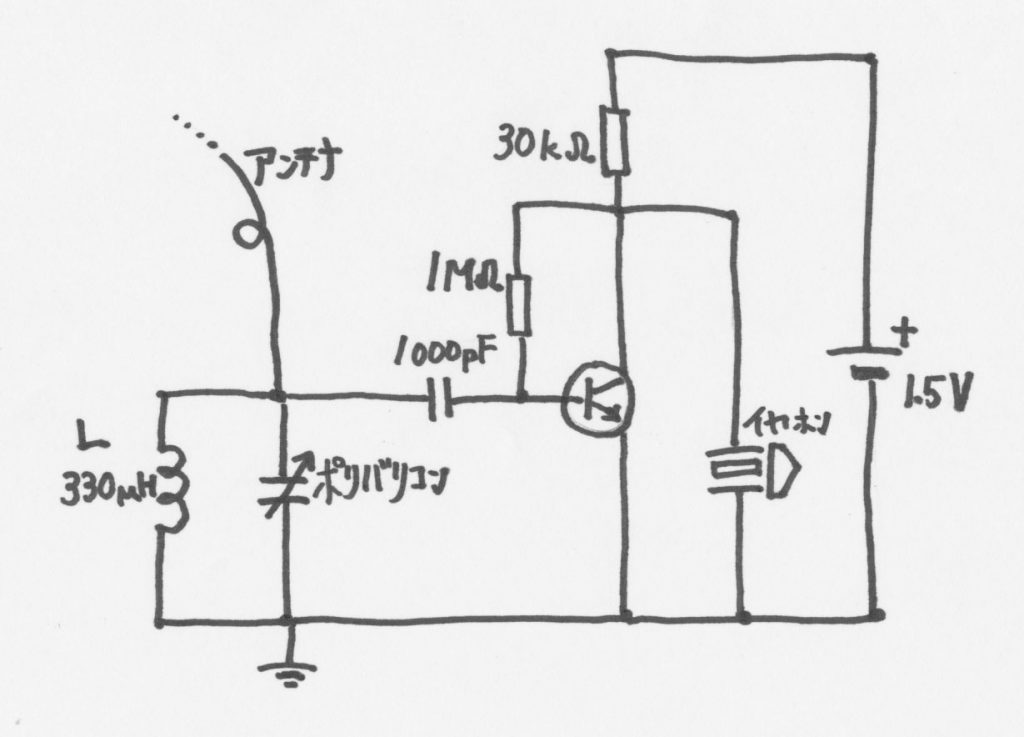
トランジスタを一個用いたラジオをとりあげます。オリジナルの回路ではなくて,シャンテック電子のキット(1石トランジスタラジオキット)をそのまま紹介するだけです。講義で先に電磁波のことを学んでいるとして,その例として簡単なラジオをとりあげます。下に,回路図を上げます。
左方面が検波のところです。コイル(\(330 \, \mu \mathrm{H}\))と バリコン が並列につながれています。右側が増幅の部分です。上記を,ブレッドボード上に組んでみました。
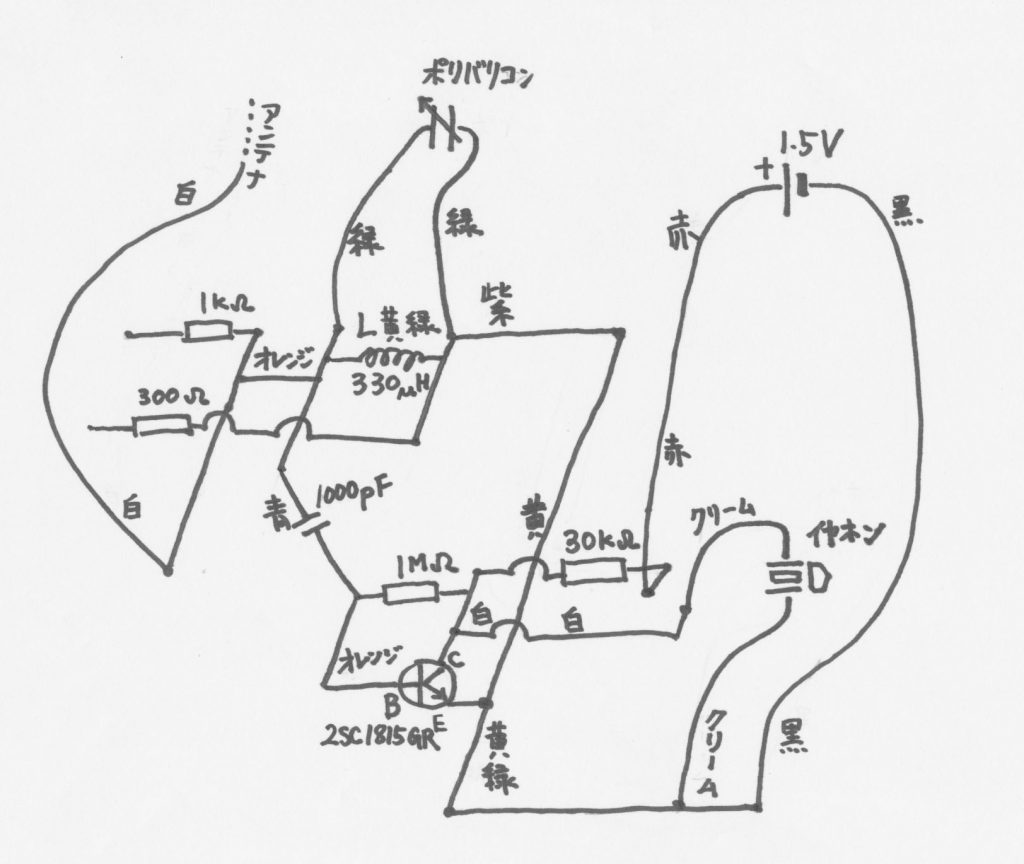
教室でのデモを考慮してやや隙間を空けてパーツを配置しています。上図を図にしてみます。
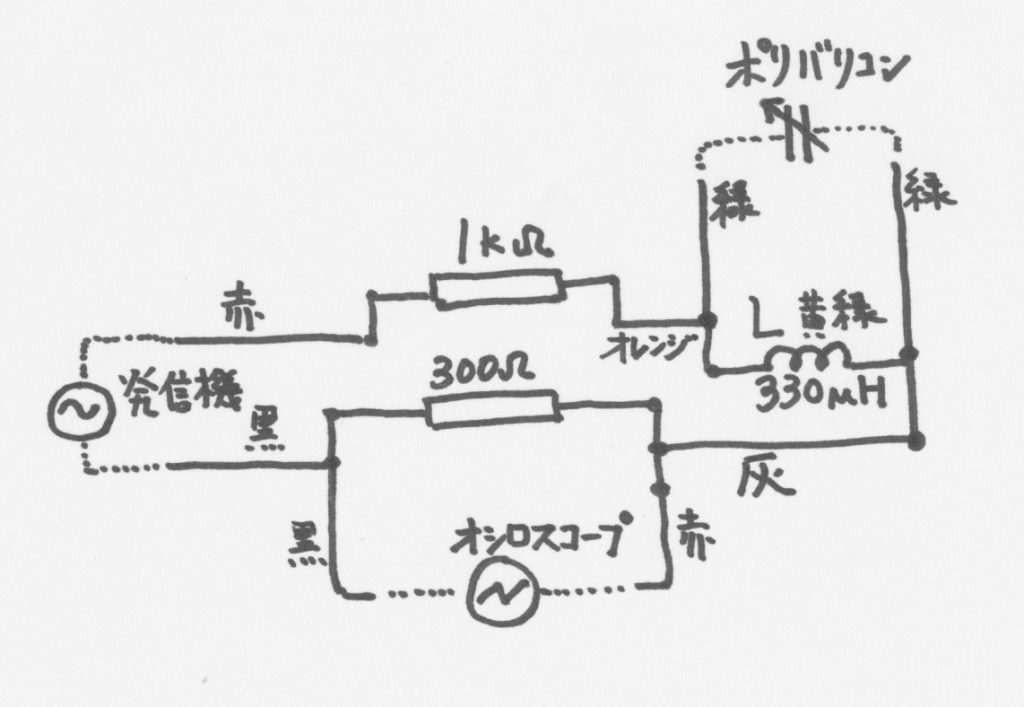
同じ回路なのですが,複雑な配線になっています。左上方面にある \(1 \, \mathrm{k \Omega}\) と \(300 \, \mathrm{\Omega}\) の抵抗は,検波の機能を見るためのもので,ラジオの回路とは関係がありません。
最初に,検波の部分を試してみます。バリコンとコイルの並列の部分だけを取り出してみました。入力は電波を拾うのではなくて,交流発信機の電圧を直接繋いで入力とします。
上の写真を図にしたものが下記。
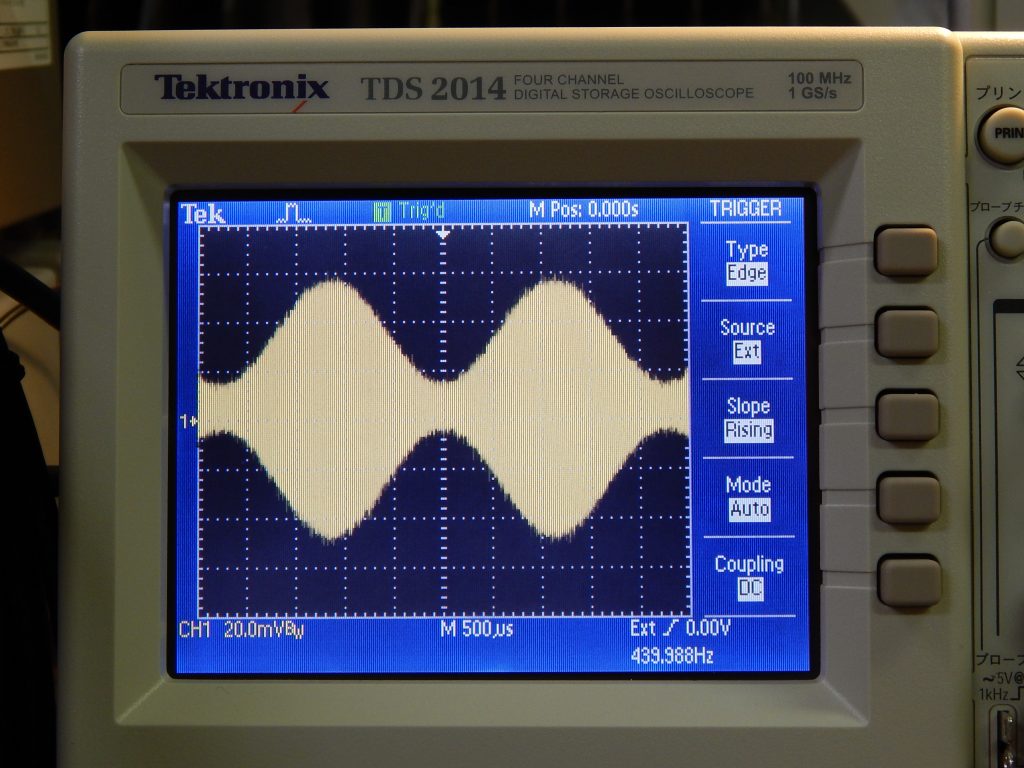
抵抗を直列に二つ繋いでいます。 \(300 \, \mathrm{\Omega}\) の抵抗の電圧をオシロで見てみます。交流発信機は 700 kHz で 440 Hz の AM 変調をかけています。出力は 1 V です。バリコンのダイヤルを適当な位置にしておくと下図のような波形です。
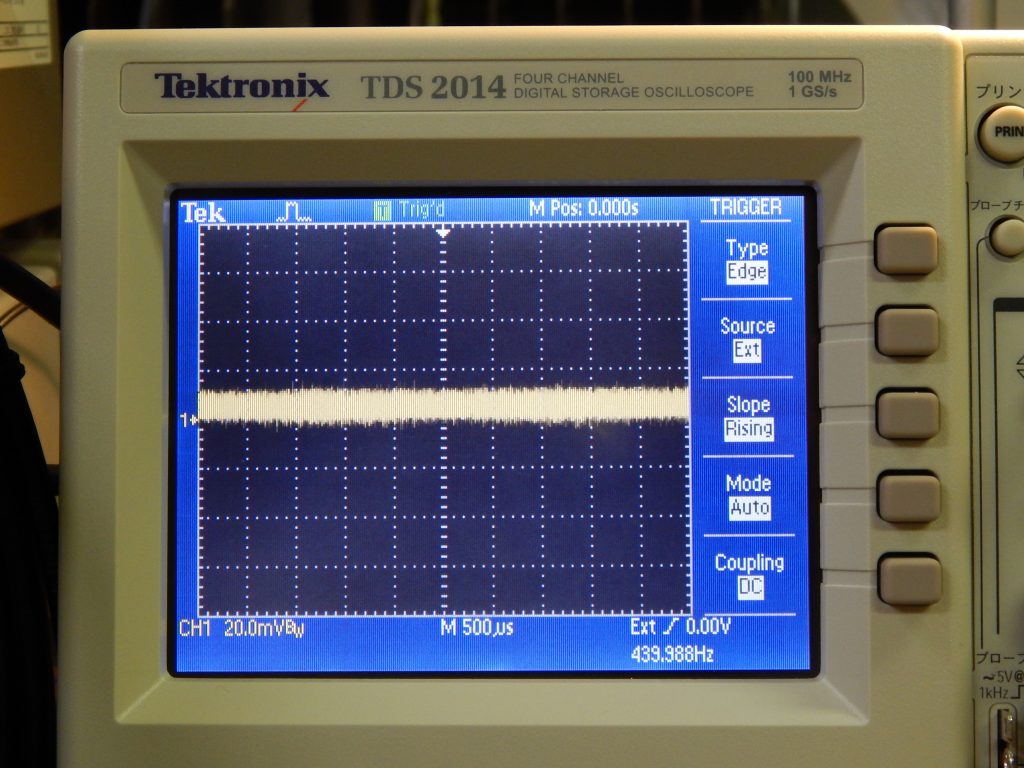
バリコンを調節して,共振の位置にすると下図のように振幅が小さくなります。
バリコンのダイヤルを回しているときの信号の変化を動画に撮影してみました。
共振周波数では L とバリコンの並列回路に流れる電流は小さくなることが分かります。
次にその後の増幅のところです。回路は最初のもの(ラジオ全体)を使います。発信機の出力は 700 kHz,440 Hz の AM 変調,0.6 V にしました。イヤホンの代わりに \(10 \, \mathrm{k \Omega}\) の抵抗を繋ぎます。一番右側にあるのが \(10 \, \mathrm{k \Omega}\) の抵抗です。
この \(10 \, \mathrm{k \Omega}\) の抵抗の電圧をオシロで見てみました。上図の下の方に見えているプローブがオシロのもので, \(10 \, \mathrm{k \Omega}\) の両端の電圧を測定しています。
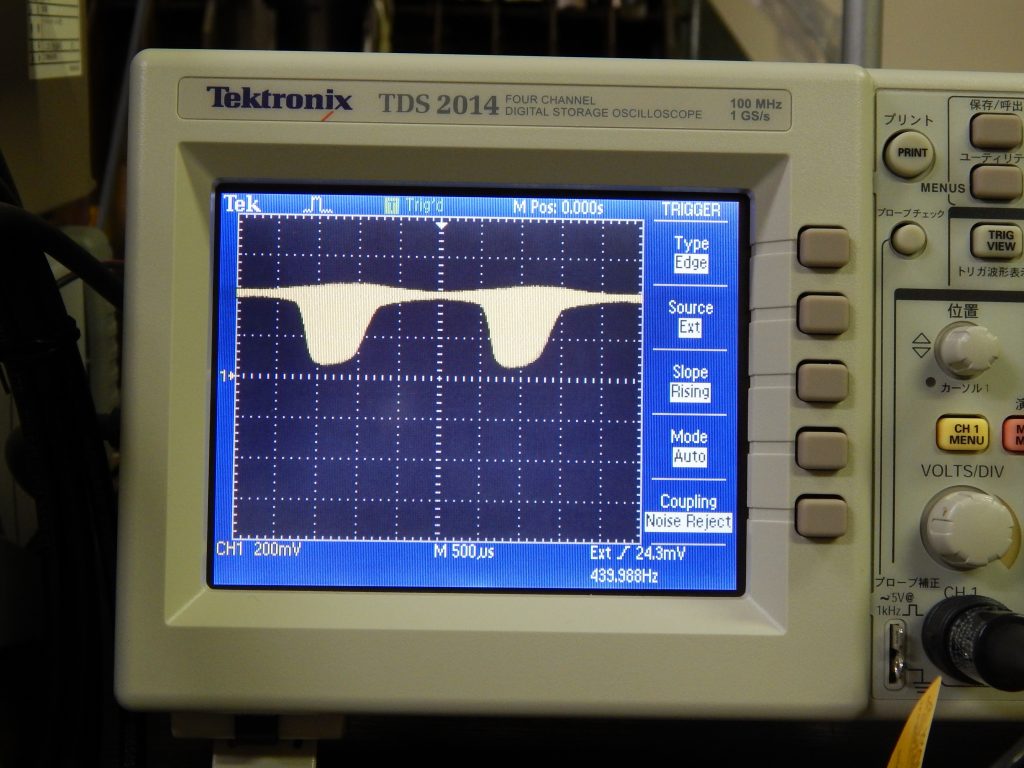
やや歪んでいますが,電圧が正の側が小さく,負の側が大きく増幅されています。全体として正電圧です。回路を考えると確かにそうなるようです。
\(10 \, \mathrm{k \Omega}\) の抵抗を \(0.47 \, \mathrm{\mu F}\) のキャパシターと交換しました。
キャパシターの両端の電圧をオシロで観測してみました。
搬送波が消えて,変調信号のみが観測されました(と言うには,かなり歪んでいるのですが)。イヤホンは圧電素子ですのでキャパシターとみなせば,その電圧もこれと同じようになっていると予想されます。またひとつ前のオシロの観測から予想されることですが全体的に電圧が正の値になっています。
このラジオを持って出かけて,アンテナとして使えそうなものを探してみました。ひとつは建物の渡り廊下の屋根が良い具合でした。
同じところですけど,もう一枚
鉄骨がアンテナになっていると思います。クリップで金属がむき出しになっているところをくわえます。あともうひとつ,建物の雨どい?です。窓から手のと届く位置にありました。
同軸のケーブルの先端にクリップを半田付けして鉤状にし,建物の中に引き込みました。
同軸ケーブルは \(20 \, \mathrm{m}\) の長さです。教室でデモをするのでかなり長くないと教卓まで届きません。この長さでも減衰は感じられませんでした。
受信しているところを,動画に撮って見ました。
マイクで,イヤホンの音が上手く拾えません。実際はかなり大きな音なのですが。
窓の外の風景です。左端が由布岳,その右に鶴見岳,右端が高崎山です。AM の送信所は高崎山の方向にあります。


































































Pingback: 電磁気学関連の動画 – kondolab