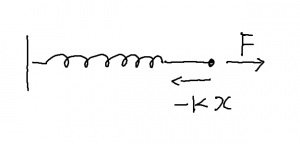力学の授業です。教科書は,永田一清著『新基礎力学』サイエンス社です。
このうち,第ゼロ章「はじめに」,第1章「運動の表し方(1)」,第2章「運動の表し方(2)」,第3章「力と運動」,第4章「いろいろな運動(1)」,第6章「エネルギーとその保存則」が講義で取り扱う範囲です。
中間テスト,期末テスト,e-Learning の課題で成績を評価します。以下,講義の内容や反省点等を書いてみます。去年の記事を少しづつ編集していきます。
0章 はじめに
最初のこの週はオンライン授業となった。去年の教材を修正して利用した。
ここはほぼ省略。力学の歴史が主な内容。アリストテレスの運動に関する理解や,その後のニュートンの話。「運動の3法則」のイントロとしては必要な内容であるが,どちらかと言えばこの内容は所々で話に織り込んでいった方が良い。
1章 運動の表し方(1)
運動学といわれる領域。運動の記述。
1.1 位置と座標系
直交座標系や右手系のことが記述されている。日頃使用しているままで,新たに再認識する必要はない。あまり内容に触れることなく,ただ座標を時間の関数として \(x(t)\) と表すことだけ話す。\( x = f(t)\) ではなくて \(x = x(t)\) と記述して,\(f\) のような名前を持ち出すことなく表記することに慣れてもらいたいということだけ話す。
1.2 2次元極座標と弧度法
極座標は,この後の講義でそれほど出てこないが,ラジアンの定義や利用方法は確認したい。定義を復習した後,例題 1.1 に飛ぶ。
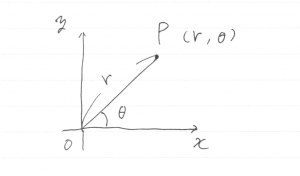
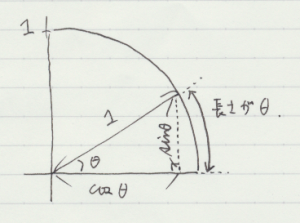
デカルト座標とは異なる位置の表し方として,極座標がある。位置を点 P として,デカルト座標の原点 O からの距離 \(r\) と \(x\) 軸と OP のなす角 \(\theta\) の二つの値で位置を示すものである。
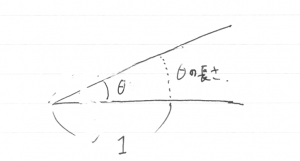
\(\theta\) として用いるのは,通常ラジアンである。ラジアンの値は,その角に対応する半径 1 の円の弧の長さである。
確認は例題 1.1 で。
例題 1.1
等速円運動の速度 \(v\) を角速度に変換する所でラジアンの定義を再度確認することが要点。
1.3 位置ベクトルと変位ベクトル
ベクトル,スカラーの話。ベクトルとは何かを話す必要はない。
物理で扱う量にはベクトル量が多く,大きさと方向を持っていて,力や速度がこれにあたる。ベクトルでないものとしては,温度やエネルギーがあり,これらは大きさのみを有していてスカラーと呼称される。
速度ベクトルは位置ベクトルと異なって,起点は重要でない。空間のどこに存在しても同じベクトルであれば区別はない。
1.4 ベクトルの基本的性質
ベクトルの和と差,成分表示など。ここも特に取り扱う必要はない。章末の演習問題をやるのみで良い。
第1章演習問題
[5] のみを取り扱った。
e-learning による課題の準備
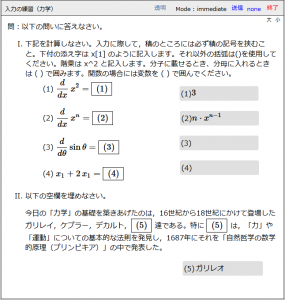
e-learning で宿題をだすので,その利用方法の説明。今回は出席の確認として利用した(下図)。
数式の入力方法と入力例を見せること,後採点なので「accepted」とだけ表示されること,何回でも送信可能であること等を話した。
このあたりで初日の終わり。オンラインなので「調査」をやることは出来なかった。
2章 運動の表し方(2)
この日から対面の授業。「調査」を実施したいので,50分ほどとられるだろう。演習などを切る必要がある。
前章の運動学の続き。前章は座標を取り扱ったが,ここでは速度,加速度を取り扱う。ただし力は取り扱わないことに注意する。放物運動も演習問題にはあるが,力との絡みはない。実質最初の講義なので,入りに悩む。何か必然的な入りがないものか。
2.1 速さ
速さに関しては,小学校の頃から,速さ=距離/時間 と教わっている。仮に 1 時間で 60 km 移動したからといって,平均的な速度が 時速 60 km というだけで,途中の速さは分からない。つまり速さは本質的に瞬間的な概念だと言える(言葉の使用に矛盾があるかも)。瞬間の速さが速さであって,瞬間という言葉を前につける必要はないのではないか。瞬間的というよりはある時刻といった方がふさわしい気がするが,それは特別なことでは無くて,先の速さの定義式の極限を考えるだけである。距離を \(s(t)\) として,
- \(\displaystyle v(t) = \lim_{\Delta t \to 0} \frac{s(t+\Delta t) – s(t)}{\Delta t}\)
この後,自由落下を用いて,上記の定義の例を示す。\(\displaystyle s(t) = \frac{1}{2} \, g \, t^2 \) であるが,
- \( \displaystyle s(t+\Delta t) – s(t) = \frac{1}{2} \, g \times 2 \, t \, \Delta t + \frac{1}{2} \, g \, \Delta t^2\)
よって,
- \(\begin{eqnarray} \displaystyle
v(t) &=& \lim_{\Delta t \to 0} \frac{s(t+\Delta t) – s(t)}{\Delta t} \\
&=& \lim_{\Delta t \to 0} \frac{1}{2} \, g \times 2 \, t + \frac{1}{2} \, g \, \Delta t \\
&=& g \, t
\end{eqnarray} \)
見慣れた式が得られた。結局時間で微分していることを強調する。この後,逆に速さから距離を積分で得る場合。
これまでは,ここに e-Learning の演習を入れていたが,今年は省略した。
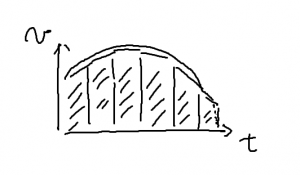
高校では,\(v – t\) グラフにおいて直線で囲まれた台形の面積を移動距離と考えていたが,そうであれば自由に変化するグラフであっても,その面積が距離でないはずがない,というような話をしておいて,ならば(面積を求める)速度の積分が座標となるはずと結論する。
- \(\displaystyle s = \int_{t_A}^{t_B} v(t) dt\)
2.2 速度
ベクトル的な速さの取り扱い方。とくにその点は問題にならないと予想する。先の 2.1 でやった移動距離の時間微分の話との関連の説明ぐらいかと思う。
速度の定義は,座標ベクトルの時間変化の極限を取ったものと定義されるが,それは各速度成分の値が座標の成分の微分となることから,定義として妥当であることが分かる。
- \(\begin{eqnarray} \displaystyle
\vec{v} &=& \frac{d \vec{r}}{d t} \\
&=& \left( \frac{d x}{d t} , \, \frac{d y}{d t} \right)
\end{eqnarray} \)
2.3 加速度
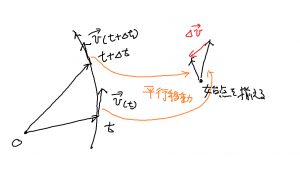
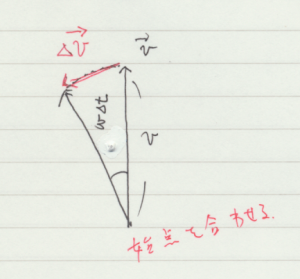
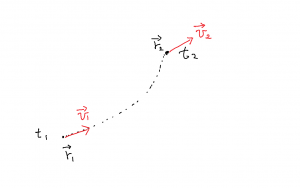
教科書では,加速度はいきなりベクトル的に取り扱う。前振りとしての直線運動の加速度の話はない。ここでは,加速度が速度の微分であることを話し,また時刻 \(t\) から \(t + \Delta t\) 間の速度の変化 \(\Delta \vec{v} = \vec{v}(t + \Delta t) – \vec{v} (t)\) を考えるときに,それぞれの速度ベクトルの始点を揃えて配置するというところを強調する。
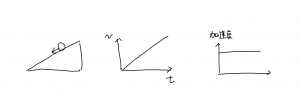
加速運動を定量的に検討したのは,ガリレオが最初であるが,有名な斜面の実験の結果,落下の速度は時間に比例して直線的に増加し,(時間に対する)加速度は一定であると分かった。運動に対する素朴なアイディアでは,力と速度を結び付けて速度が増加する時働く力も増加しているかのように考える傾向があるが,斜面上では働く力は一定で,速度の増加と対応しない。むしろ一定の力と対応するのは(一定の)加速度の方である。このような話をイントロとした。
加速度の定義をまずはしなければならないが,これはとりあえず1次元的な直線運動の加速度から始めると良いのかもしれない(今年はそうしなかった)。速度変化を時間で割って加速度とするが,それは結局下記のような加速度と速度の微分の関係に帰結する。
- \(\displaystyle a = \frac{d v}{d t} \)
2次元的な運動では,天下り的に,速度ベクトルの変化を時間で割ったものとして定義を与えた。また速度ベクトルを平行移動して始点を揃えて,その変化量を考えることを強調した。
上記のような,2次元平面上の加速度の定義が妥当であることは,その成分を見てみると分かる。下記に示すような,それぞれの成分の時間微分となっていて,1次元の話とつながる。
- \(\displaystyle \vec{a} = \left( \frac{d v_x}{d t} , \, \frac{d v_y}{d t} \right)\)
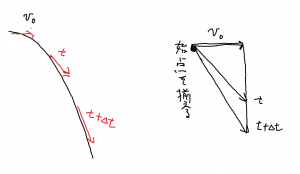
始点を揃えて速度の変化量を考えることの例として,放物運動を取りあげた。
水平方向の速度は一定で,鉛直方向の速度のみ変化する例である。これを定義に従って計算し加速度を求めと,下記のような見慣れた値が得られる。
- \(\displaystyle \vec{a} = \left( 0 , \, – g \right)\)
このあたりで2日目の終わり。この日 FCI を実施した。
2.4 等加速度運動
先週,座標,速度,加速度が微分や積分で関係していることを話していて,でも具体的には何もとり扱っていない。そこで例として加速度が一定となる場合に微積の関係がどうなるのか見てみるという位置づけかと思う。教科書では,加速度から速度を求めて次に座標という順に,積分していく方向で取り扱っている。
等加速度運動を例にとって,加速度から始めて速度,座標との関係(積分による繋がり)をみる。
\(a -t\) グラフは水平な直線となり,直線下方の面積が速度となる。
- \(\displaystyle \mathrm{加速度} = a\)
\(v -t\) グラフは 1 次関数の直線となり,切片が初速で傾きが加速度。直線下方の面積が座標となる。
- \(\displaystyle v(t) = a \, t + v_0\)
\(x -t\) グラフは 2 次関数となり,切片が始点で傾きが速度, \(t = 0\) での傾きは初速。直線下方の面積は不明。
- \(\displaystyle x(t) = \frac{1}{2} \, a \, t^2 + v_0 \, t + x_0\)
(2.5) 等速円運動
等速円運動を例として,先週の加速度の定義,特に視点を揃える点を考えてみるという位置づけで取り扱う。
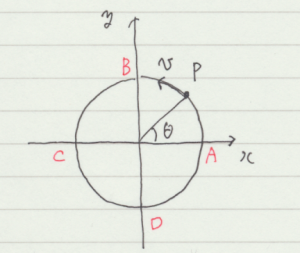
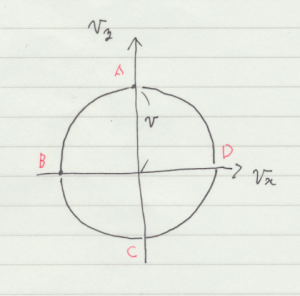
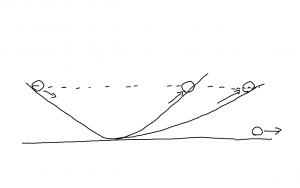
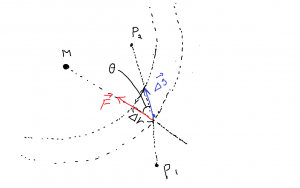
下図のように,半径 \(r\) の円周上を点 P が速度 \(v\) で運動している。
図中の\(\theta\) は時間に対して一定の割合で増加するが,この増加分(角速度)を \(\omega\) とする。 \(r, \, v\),\(\theta\),\(\omega\) の間には \( \theta = \omega \, t, \quad v = r \, \omega\) が成り立ちます。以下,等速円運動の速度と加速度に関して考える。
ここで,速度を座標としてプロットしたホドグラフという図(上図)を利用する。fig. 2.5.1 で \(x\) 軸上の点 A に質点があるとき,ホドグラフ上では \(y\) 軸上にある。この図を使って,点 A での加速度を考える。
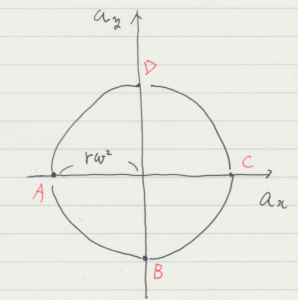
質点が点 A の位置にあるときと \(\Delta t\) 秒経過した時刻との間での速度変化を考える。点 A の時刻において,ホドグラフ上で \(y\) 軸方向を向いていた速度は左側に倒れるように,\(\omega \Delta t\) 回転している。この速度変化 \(\vec{\Delta v}\) は,大きさが \(| \vec{\Delta v} | = r \, {\omega}^2 \, \Delta t\) である。それゆえ加速度 \(\vec{a}\) の大きさは
- \(\begin{eqnarray} \displaystyle | \vec{a} | &=& \frac{| \vec{\Delta v} |}{\Delta t} \\ &=& r \, {\omega}^2 . \end{eqnarray}\)
その向きは,水平方向左向きであるが, fig. 2.5.1 に戻って考えると,円運動の中心を向いている。前週に,速度変化を考えるとき速度ベクトルの始点を揃えて比較するということだったが,ホドグラフを使うと自動的に始点を揃えて考えている。加速度のグラフを fig. 2.5.3 に示す。
例題 2.1
(1) は座標を表す式が与えられて,速度や加速度を求めるもの。微分して行く方は分かりやすいと思う。
(2) は速度が与えられて,移動距離を求める。積分する方である。速度の式は下記。
- \(v(t) = v_0 – a \, t.\)
速度がゼロとなる時刻を \(t_0\) として (\(t_0 = v_0 / a\)),\(t_A \lt t_0 \lt t_B\) となる時刻 \(t_A\) から時刻 \(t_B\) までの,のべの走行距離を求める。教科書の解答に誤植があるので注意。正誤表にあるのだが,下記が正しい解答。
- \(\displaystyle \frac{a}{2} \, \left\{ \left( t_0 – t_A \right)^2 + \left( t_B – t_0 \right)^2 \right\}\)
例題 2.2
この例題は極座標における速度や加速度の表現を考えるもの。座標系を変更する時に運動の表し方がどのように変わるのかということであるが,座標系を変更する必然性の説明が難しい。円運動や中心力の場合に便利ということを話すだけでは十分ではないと感じている。まだ運動の法則(力学の始まり)までたどり着いていないが,デカルト座標系以外の力学の記述方法があるということを知る点が本当の話の中心ではないか。つまり一般化座標の話であって,もともとがそういう話ではあるので,もう少しあとに配置してもよい内容なのかもしれない。
ここは,極座標での速度や加速度の表し方を扱う。先に,速度は座標の時間微分 \(\displaystyle \left( \frac{d x}{d t} , \frac{d y}{d t} \right)\) で表された。しかし極座標では \(\displaystyle \frac{d r}{d t} \) は速度であるが \(\displaystyle \frac{d \theta}{d t} \) は速度を表さない。加えて極座標を用いる場合も速度はベクトルであるが,その成分を考えるためには,まず成分を決めるための方向を定める必要がある。
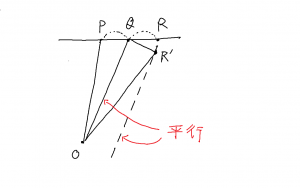
デカルト座標では, \(x\) の値が増加する時に点の座標が移動する方向を \(x\) 成分の基本ベクトルの向きとしている。極座標でも \(r, \theta\) が増加する時の座標点が移動する向きで基本ベクトルを定める。
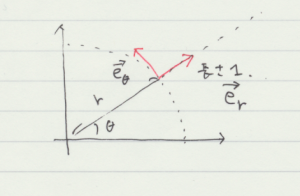
それゆえ,質点が上図のように原点からの距離 \(r\) で,\(x\) 軸との角度 \(\theta\) にあるとき,その基本ベクトル \(\vec{e_{r}}\) と \(\vec{e_{\theta}}\) は
- \(\begin{eqnarray} \displaystyle \vec{e_{r}} &=& \left( \cos \theta , \, \sin \theta \right) \\ \vec{e_{\theta}} &=& \left( – \sin \theta , \, \cos \theta \right) . \end{eqnarray}\)
このベクトルは点がどこにあるかによって異なるものとなる。それゆえ質点が運動する場合などには時間変化するということで,教科書では問題(1)として, \(\vec{e_{r}}\) と \(\vec{e_{\theta}}\) の時間変化を求めている。
- \(\begin{eqnarray} \displaystyle
\frac{d \vec{e_{r}}}{d t} &=& \left( \frac{d \cos \theta}{d t} , \, \frac{d \sin \theta}{d t} \right) \\
&=& \left( – \sin \theta \, \frac{d \theta}{d t} , \, \cos \theta \, \frac{d \theta}{d t} \right) \\
&=& \frac{d \theta}{d t} \, \left( – \sin \theta , \, \cos \theta \right) \\
&=& \frac{d \theta}{d t} \, \vec{e_{\theta}}
\end{eqnarray}\)
同様にして
- \(\begin{eqnarray} \displaystyle
\frac{d \vec{e_{\theta}}}{d t} = – \frac{d \theta}{d t} \, \vec{e_{r}} . \\
\end{eqnarray}\)
問題(2)では円運動の場合の速度ベクトルや加速度ベクトルを求める。以下では,教科書とは異なるが,円運動に限定せず極座標における一般的な速度ベクトルを考えてみる。
極座標における位置ベクトル \(\vec{r}\) は,\(\vec{r} = r \, \vec{e_{r}}\) と表されるので,これを時間微分して速度を求める。
- \(\begin{eqnarray} \displaystyle
\vec{v} &=& \frac{d \vec{r}}{d t} \\
&=& \frac{d r}{d t} \, \vec{e_{r}} + r \, \frac{d \vec{e_{r}}}{d t}\\
&=& \frac{d r}{d t} \, \vec{e_{r}} + r \, \frac{d \theta}{d t} \, \vec{e_{\theta}}
\end{eqnarray}\)
上記の様に,極座標で速度を考えるとすぐに基本ベクトルの時間微分が出てくる。加速度を考えると下記のように \(\vec{e_{\theta}}\) の時間微分も出てくる。
- \(\begin{eqnarray} \displaystyle
\vec{a} &=& \frac{d \vec{v}}{d t} \\
&=& \frac{d}{d t} \left\{ \frac{d r}{d t} \, \vec{e_{r}} + r \, \frac{d \theta}{d t} \, \vec{e_{\theta}} \right\} \\
&=& \frac{d^2 r}{d t^2} \, \vec{e_{r}} + 2 \, \frac{d r}{d t} \, \frac{d \theta}{d t} \, \vec{e_{\theta}} + r \, \frac{d^2 \theta}{d t^2} \, \vec{e_{\theta}} – r \, \left( \frac{d \theta}{d t} \right)^2 \, \vec{e_{r}}\\
&=& \left\{ \frac{d^2r}{dt^2} – r \, \left( \frac{d \theta}{d t} \right)^2\right\} \, \vec{e_r} + \left\{ 2 \, \frac{d r}{d t} \, \frac{d \theta}{d t} + r \, \frac{d^2 \theta}{d t^2} \right\} \, \vec{e_{\theta}}
\end{eqnarray}\)
結局,基底が変わるのに合わせて,速度や加速度を別な基底で表しただけ(基底の向きが変わる)。変数に関しても \(x\) や \(y\),\(\displaystyle \frac{d x}{d t} \) を使うのではなく, \(r\) , \(\theta\),\(\displaystyle \frac{d r}{d t} \) 等でその成分を表現している。
- \(\displaystyle \left( v_r, v_{\theta} \right) = \left( \frac{d r}{d t}, r \, \frac{d \theta}{d t} \right)\)
上記のように書くと,通常この形はデカルト座標の \(x\) 成分や \(y\) 成分を表すときに使うので,誤解を生じるかもしれない。
このあたりで3日目の終わり。
2章演習問題
[3]
1次元の運動で座標の時間変化がグラフとして与えられている。(1) はグラフから平均の速度を求める。(2) はグラフから速度を求める問題だがグラフに接線を引く必要があり,曖昧な解答になる。(4) の後で解答しても良い。(3) はグラフの式を求める問題。2次式であると限定されているので明確に定まる。(4) は等加速度運動であることを示す問題。微分して速度を出し,速度を微分して加速度を出す。微分を使うところが演習のポイント。
[4]
\({v_1}^2 – {v_2}^2 = 2 \, a \, s\) を導く問題。この式は思い出しておいた方が良い。6章のエネルギーの話にも繋がる。
[6] の(3)
下記では,デカルト座標での \(x, y\) 成分を時間で微分して速度や加速度を得る。これとは別に例題 2.2 のところで導いた式を利用しても良いだろう。例題 2.2 を取り扱うときに円運動に限定せず一般的な運動として極座標での速度加速度の式を組み立てたので,それがここで利用できる。
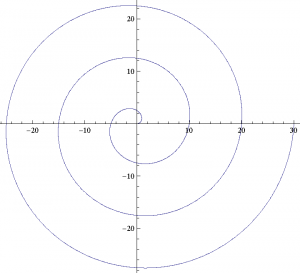
螺旋運動の軌道,速度,加速度を求める問題。座標は以下の様な式で表される。
- \(\begin{eqnarray} \displaystyle
x &=& v_0 \, t \cos \omega \, t \\
y &=& v_0 \, t \sin \omega \, t
\end{eqnarray}\)
コンピューターで軌跡を描いてみる。
極座標で考えるが, \(r = v_0 \, t\) で,また \(\theta = \omega \, t\) 。これから軌跡の式として下記が得られる。
- \(\displaystyle
r = \frac{v_0}{\omega} \, \theta
\)
角度と原点からの距離が比例している式である。しかし軌跡のイメージは難しい。速度を求める。
- \(\begin{eqnarray} \displaystyle
v_x &=& \frac{d x}{d t} \\
&=& v_0 \, \cos \omega \, t – \omega \, v_0 \, t \, \sin \omega \, t\\
v_y &=& \frac{d y}{d t} \\
&=& v_0 \, \sin \omega \, t + \omega \, v_0 \, t \, \cos \omega \, t\\
\end{eqnarray}\)
よって速度ベクトルは
- \(\begin{eqnarray} \displaystyle
\vec{v} &=& \left( v_x , \, v_y \right) \\
&=& v_0 \, \left( \cos \omega \, t , \, \sin \omega \, t \right) + \omega \, v_0 \, t \, \left( – \sin \omega \, t , \, \cos \omega \, t \right)\\
&=& v_0 \, \vec{e_r} + \omega \, v_0 \, t \, \vec{e_{\theta}}
\end{eqnarray}\)
この式は先ほどの例題 2.2 で導いた極座標の速度の式 \(\displaystyle \vec{v} = \frac{d r}{d t} \, \vec{e_{r}} + r \, \frac{d \theta}{d t} \, \vec{e_{\theta}} \) と比較される式である。この螺旋の式の場合 \(r = v_0 \, t\) で, \(\theta = \omega \, t\) であるので,確かに \(\displaystyle \frac{d r}{d t} = v_0\) で \(\displaystyle r \, \frac{d \theta}{d t} = v_0 \, t \, \omega\) となっていて先の計算の通り。
加速度を求める。
- \(\begin{eqnarray} \displaystyle
a_x &=& \frac{d v_x}{d t} \\
&=& – 2 \, \omega \, v_0 \, \sin \omega \, t – {\omega}^2 \, v_0 \, t \, \cos \omega \, t\\
a_y &=& \frac{d v_y}{d t} \\
&=& 2 \, \omega \, v_0 \, \cos \omega \, t – {\omega}^2 \, v_0 \, t \, \sin \omega \, t\\
\end{eqnarray}\)
よって加速度ベクトルは
- \(\begin{eqnarray} \displaystyle
\vec{a} &=& \left( a_x , \, a_y \right) \\
&=& 2 \, \omega \, v_0 \, \left( – \sin \omega \, t , \, \cos \omega \, t \right) – {\omega}^2 \, v_0 \, t \, \left( \cos \omega \, t , \, \sin \omega \, t \right)\\
&=& 2 \, \omega \, v_0 \, \vec{e_{\theta}} – {\omega}^2 \, v_0 \, t \, \vec{e_r}
\end{eqnarray}\)
\(r = v_0 \, t\) であることを考えると後ろの項は円運動の向心加速度である。前の項は形から言えばコリオリ力に関する加速度のように見える。
加速度のとらえ方に戸惑うところ。このような加速度であるということは,この螺旋運動をするためには,このような加速度,つまり力が必要だと考えるべきか。
例題 2.2 で導いた極座標の加速度の式は,
- \(\displaystyle
\vec{a} = \left\{ \frac{d^2r}{dt^2} – r \, \left( \frac{d \theta}{d t} \right)^2\right\} \, \vec{e_r} + \left\{ 2 \, \frac{d r}{d t} \, \frac{d \theta}{d t} + r \, \frac{d^2 \theta}{d t^2} \right\} \, \vec{e_{\theta}}\)
この螺旋の式の場合 \(r = v_0 \, t\) で, \(\theta = \omega \, t\) であり,よって \(\displaystyle \frac{d r}{d t} = v_0\) , \(\displaystyle \frac{d^2 r}{d t^2} = 0\) , \(\displaystyle \frac{d \theta}{d t} = \omega\),\(\displaystyle \frac{d^2 \theta}{d t^2} = 0\) となって,これを上式に代入すれば先と同じ結果を得る。
[8]
等速円運動の問題。半径が不明の円形道路を自動車が \(72 \mathrm{km/h}\) で走る。角速度,円の半径,向心加速度を求める。
e-learning 練習問題01
教科書とは別に e-learning で練習問題を実施する。下記がその問題。演習としては簡単なものであるが,次の3章で運動の法則に入るので,ガリレオの話をするところだと思う。
ガリレオは重力による落下運動を一様な加速運動と考えたが,一様な加速には二つの可能性があると考えた。ひとつは落下距離に比例して速度が増加する場合と,もうひとつは時間に比例して速度が増加する場合である。しかし距離に比例する場合には,どのような距離を落下する場合にも必要となる時間が同じ時間となり観察と矛盾する(距離に比例する速度となる場合は単振り子の運動のような場合。振幅に関わらず周期が同じ)。それでもうひとつの時間に比例するとして仮説を立て,有名な斜面の実験を試みた。その実験では物体が通過する距離とそれにかかる時間の関係を観測したが,また別の方法でも実験していて,それが上の問題にある等しい時間間隔で音を鳴らすようにベルを配置する実験である。\(v – t\) グラフを書いてその面積を使って考えればすぐ分かるが,ベルの間隔は奇数の並びとなる。
3章 力と運動
運動学から力学へと切り替わる章である。これまでところ力に関する記述としては,ゼロ章に「日常経験に基づいた常識的な力の概念を用いて話を進める」とある。学生は高校で力学を学んでいるので,日常経験以外にも力に関してすでに何らかのアイディアを有しているだろう。アリストテレス的な力学では地表面の重力を力とはみなさず,落下運動は自然な運動と考えていた。摩擦力や垂直抗力も力とはみなしていなかっただろうし,万有引力はその存在も意識していない。講義ではこれらすべてを最初から力として語る。力という言葉にどんな意味を負わせているのか。
運動学からニュートンの三法則への展開は,物理を初めて学ぶ人にはどのように見えるのだろうか。三法則を公理として力学を展開していく構成だという意見もある。しかし,この三法則によって力学的現象の見通しが良くなるという感覚はない。公理には元来そのような役割はないのかもしれないが。
3.1 ニュートンの第1法則(慣性の法則)
慣性の法則とは,一般的には「物体は力が働かなければ,速度が変化しない」と言った内容である。例年歴史的な話から始めている。慣性系の話はこれまでやってこなかったが,本当はそこが重要なのかもしれない。慣性の法則を中心にして話を組みなおすとどうなるのか?
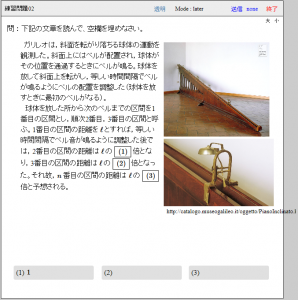
アリストテレスの力学では,力が強ければ速さも大きい。力が止めば運動も止まる,という理解であった。日常的には妥当であるが,ただそれでは説明できない現象もある。例えばボールを投げるとき,手を離れたボールが飛び続けるのは何故かといった問いには答えることができない。
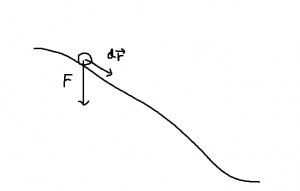
これに対し,ガリレオは以下のような主張をする。坂道を下ったボールが摩擦で勢いを失うことがなければ,また同じ高さまで坂道をのぼると考えられることから(上図),のぼり坂の傾きをゆるくするとより遠くまでボールが進むことになる。それなら坂の傾きがなくなった水平の状態では減速せずどこまでもボールが進み続けると結論する。つまり運動は本来持続するものだという主張であるが,ニュートン以前に,すでにこのような理解があった。
慣性の法則を,“力と速度は関係がない”と言い表すと,その歴史的文脈での役割がはっきりするように思える。力によって運動は生じるが,速度や力という概念を明確に定義するレベルに達したとき,力と速度は無関係であると考える段階に入ったということではないか。それでは,力と関係しているのは何か。それが運動の第2法則で述べられる。
3.2 ニュートンの第2法則(運動方程式)
ガリレオは斜面での落下運動を考察した。斜面の傾きを大きくすると加速度も大きくなる。これは斜面に沿って物体を引く力が大きくなるからであるが,その力の大きさは斜面上に物体を静止させるときに必要となる力で示される(下図)。

https://catalogue.museogalileo.it/gallery/PlaneWithVariableInclinationInv1402.html
これから,力と加速度の関係が推察される。一方で,ガリレオは重い物体も軽い物体も落下速度は同じということを知っていた。重さが2倍になると力も2倍になるから,加速度が同じであると言うことは物体の重さ自体に加速度を減少させる働きがあることになる。このような所から下記の関係が導かれて来たのだと推察される。
- \(\displaystyle \mathrm{加速度} \propto \frac{\mathrm{力}}{\mathrm{質量}} \)
地球上の重力に限らず,万有引力のもとでの運動は物体の質量に依存しない。地球も小さな石ころも太陽の引力のもとでは同じ軌道をたどり,同じ幾何学的な軌跡を描く。
ニュートンは第2法則を“運動の変化が力に比例”と表現していて(変化率ではない),それは式で表現すれば
- \(\displaystyle m \, \Delta v = \vec{F} \, \Delta t.\)
“力に比例”における“力”も力積を表している。
教科書ではここで運動量変化と力積の関係が述べられる。力が一定時間継続する場合に運動方程式の両辺を時間で積分して得られる関係である。時間が長くなったけれどもその関係式の意味するところにはあまり変化がない。
力積を使った話としては面積速度一定の話がある。
このときは力積で考えている。これによって運動量を導入することも考えられる。
3.3 ニュートンの第3法則(作用反作用の法則)
この法則が最も説明が難しい。第1法則では速度と力は関係がない,第2では力と関係するのは加速度だと話を進めたが,第3の作用反作用の法則はどのような位置づけなのか。
作用反作用が意識されるきっかけは衝突の問題だったのかもしれない。衝突に関してはホイヘンスの研究があって,ニュートン以前から議論されている。
衝突の際,物体が速度を得るとき,逆にもう一方の物体は速度を失う。速度の変化量はそれぞれの質量に依存するが,運動量の変化は同じ大きさで反対向きである(高校で運動量保存を学んでいて,衝突の問題を解く際には運動量保存の式を立てるので,失う量と得る量が等しいことに学生は納得するだろう)。これは第2法則と合わせて考えると,2物体に反対向きの力が作用したことを意味する。つまり \(\displaystyle m \, \Delta v = \vec{F} \, \Delta t\) から,運動量の変化が等しければ力積が等しく,また衝突にかかる時間も共通しているはずであるから,力も等しくなる。
しかし,第1,第2法則からのつながりという点は明確ではない。第1法則と第2法則では“力”という言葉は現れるが,それは抽象的に扱われているように思える。力というものが物体の外部にあって物体と無関係な何か抽象的な作用として扱われているように思える。力学における力とは万有引力や衝突などで作用する力であって,遠隔的であったり近接作用であったりするが,いずれにせよ他の物体によってもたらされる作用である。ふたつ物体が存在しなければ,力も存在しない。第1,第2法則では一つの物体のみ取り扱うが,第3法則では初めて二つの物体が登場する。二つの物体がお互いに力を及ぼしあうときのルールを定めて,力学的世界が完成するといったところだろうか。
衝突以外にも摩擦や万有引力電気的な力など,作用反作用の他の例も講義において取り上げた方が良いのではないか。
(つけたし)
運動の3法則において,特に作用反作用の法則の位置づけが把握できていない。適当なストーリーの中に位置づけることができない。それに関する一つの試み。
単純な状況から始めて,力学的世界を作り上げていくことを考えてみる。ちからとは二つの物体間の相互作用であることからすると,物体が存在しないところから考えてみたらどうか。
(1) 最初は空間のみがあって,物体が存在しない。この時,力学は存在しない。
(2) 次に,空間があって,そこに物体がひとつある。この時ちからは存在しない。ちからは二つの物体が存在しないとあり得ない。この世界は慣性の法則のみ。
(3) 空間と,そこに二つの物体があるなら,お互いに他の存在の影響を考慮する必要が生じる。それが第3法則。物体を入れ替えても同じ現象となるように,対称的な法則が要求される。第2法則はこの後で良い。
(メモ:作用反作用の法則は対称性と関連があるかもしれないが,異なる質量の物体における対称性とは何か。対称性が成立しそうなのは運動量だけではないかと思える。等量の運動量変化なので対称的である。)
力学的世界のプログラミングでもするならば,第2法則と第3法則の順番を入れ替えた方がプログラミング的かもしれない。作用反作用則は様々な様態のちからを内包する入れ物。
3.4 いろいろな力
以下,3章の終わりに向けて,万有引力,垂直抗力,摩擦力,弾力(バネの力)が例示される。どれも既習の内容だけに新奇性を加えることが難しく思える。本筋ではないかもしれないが,歴史的なことを取り入れたらどうか。万有引力に関しては,ニュートンによって発見された,地球表面での重力と月の公転の向心力の関係がある。垂直抗力に関しては,これを力だと認識するところに,飛躍があると思う。この歴史的流れを調査するべきか。摩擦力に関しても,これを力として運動の様態から分離したところが重要ではなかったか。摩擦力を分離しなければ,運動は力を加えるのを止めるとそのうち静止するものとして理解される。万有引力も垂直抗力も摩擦力も,最初は力だと認識されていなかった。これらが力と認識されていく過程が力学の成立とかかわっているように思える。
万有引力
円運動の加速度 \(\displaystyle \frac{v^2}{r}\) はホイヘンスが見つけている。運動の第2法則から対応する力 \(\vec{F}\) が分かるが,これとケプラーの第3法則 \(T^2 \propto r^3\) を組み合わせると逆2乗則が得られる。
- \(\begin{eqnarray} \displaystyle
\vec{F} &\propto& \frac{v^2}{r} \\
&\propto& \frac{1}{r} \, \left( \frac{2 \, \pi \, r}{T} \right)^2\\
&\propto& \frac{1}{r^2}
\end{eqnarray}\)
太陽と惑星間の引力が軌道半径の逆2乗に比例することが導かれた。
ここで地球と月の関係を考える。月の軌道半径は \(r = 3.85 \times 10^8 \,\mathrm{m}\) ,公転周期は \(T = 27.3 \,\mathrm{日}\) 。よって速度は \(v = 1025 \,\mathrm{m/s}\) 。これから加速度 \(a\) は
- \(\begin{eqnarray} \displaystyle
a &=& \frac{v^2}{r} \\
&=& 0.00273 … \,\mathrm{m/s^2}
\end{eqnarray}\)
地球上の重力加速度が \(g = 9.80 \,\mathrm{m/s^2}\) であり,これを地球の引力によるものと解釈する。地球の半径は \(R = 6.37 \times 10^6 \,\mathrm{m}\) で,月の軌道半径のところでこの引力が,太陽と惑星間の力と同じように,距離の二乗に反比例して弱くなるとすると
- \(\begin{eqnarray} \displaystyle
g \, \left( \frac{R}{r} \right)^2 &=& 9.80 \times \left( \frac{6.37 \times 10^6}{3.85 \times 10^8} \right)^2\\
&=& 0.00268 … \mathrm{m/s^2}
\end{eqnarray}\)
ほぼ同じ値になる。これから地球の重力と太陽ー惑星間の引力が同一の性質を持つものであると結論できる。
どこかできちんとした万有引力の式を見せること。全員が力学をきちんと学んできたわけではない。
- \(\displaystyle F = – G \, \frac{M \, m}{r^2}\)
重さ
ここでは,重さと質量の違いを確認するぐらいか。高校の物理でも扱う内容であり,学生もその違いを意識していると思われる。今週の課題として関連する問題を課した。
重さとは物体が星の中心に向かって引き寄せられる力のことであり,地表においては \(m \, g\) である。アリストテレスの理論では物体が落ちるのは自然な運動と考えられていて,強制的な力による運動と区別されていた。つまり,その頃重さは力とみなされていなかった。そのような段階から今の力学までは,おおきな隔たりがあるように思える。
月面では加速度が \(1.67 \, \mathrm{m/s^2}\) で \(g\) に相当する部分が小さいので重さも小さくなる。地球の周りを周回する人工衛星や宇宙船の中では重さはゼロになる。 \(g\) が異なると,体重を秤で測定することはできない。下のリンクは国際宇宙ステーションでの体重測定の様子である。
加速度を測っているとテロップにある。 \(F = m \, a\) を利用するならば \(g\) が変化する影響は避けられる。他に変化しない例として,ばねに吊るされた錘の振動周期がある。 \(\displaystyle 2 \, \pi \sqrt{\frac{m}{k}}\) で,式に \(g\) が表れないので,測定する場所の重力の影響はない。
垂直抗力
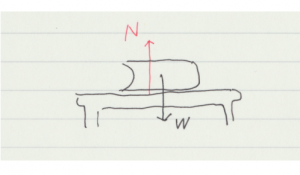
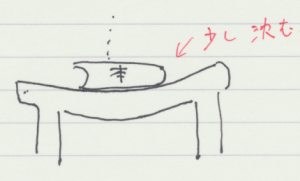
これは納得しにくい力である。机の上に本があるとして,本の重さが机を押しているのは分かるが,机が本を押し返しているのは分かりにくい。本が秤に載せられているときのように,バネで支えられているならまだ分かりやすいのかもしれない。
もう少しミクロなレベルで観測すれば,本の重さによって机もわずかにへこんでいることが分かる(観測したことはないけれども)。実際はその弾性の力で机は押し返していると考えて良い。ただその変形を考えることにあまり意味がなく無視して取り扱う。糸の張力も同じである。糸は力が加わることでわずかに伸びているが,その変形を考えても運動を考える上では意味がないと言うことで,伸びを無視して取り扱う。こういった力は束縛力といわれる。
摩擦力
アリストテレス的な力学では,重いものほど速く落下する,力を加えるのを止めると物体の運動は停止する,などと考えられていた。このような現象が観測される理由は,空気抵抗や摩擦が存在する故である。摩擦の効果を運動の本性から分離しなければ,力学は構築できなかったであろう。
摩擦力の解説はせず,例題3.2へ進んだ。
例題 3.2
内容はパス。
弾力
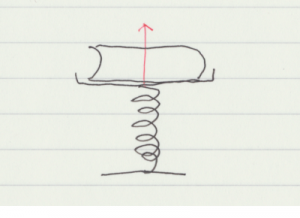
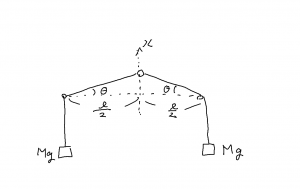
変形を元に戻す際の力であるが,これはほぼ学生は知っていることと思う。下記のような問題を考えるぐらいでどうか。
結構間違う。とくに両側におもりをつるした場合に二倍伸びると考える学生が一定数居る。
例題 3.1
(1) ケプラーの第3法則を導く問題。万有引力の式が分かっているものとする。円運動の加速度と運動の第2法則から, \(T^2 \propto r^3\) を求める。
(2)はパスした。
(3) は取り扱う。同じ物体が地球と太陽で異なる重さとなる例。
3章演習問題 [3]
飛行機の加速度を考える問題。(1) はエンジンの出力と質量から加速度を導く。(2) では乗客が受ける力を求める。(2) は重力と慣性力の合力を考えるところではないかと思うが教科書の答えは異なる。
3章演習問題 [4]
3キログラムの物体が一定の力を受けて,4秒間で4メートル進む。この時の力を求める。等加速度運動なので,最終的な速度の半分で4秒間進む場合と同じ移動距離。そこから最終的な速度を得る。初速はゼロであるので、運動量変化が分かるが、それは力積と等しいから力が得られる。
3章演習問題 [5]
エレベーターの中で鞄を提げているという状況で,上昇下降時の腕に加わる力を求める問題。最初に運動方程式を立てる。後は上昇時,下降時の加速度をあてはめる。
演習問題 [6],[7] はやらなかった。
4章 いろいろな運動(1)
4.1 重力のもとでの運動1(放物運動)
地表での重力による運動に関する話。放物線となることは高校で十分に学習済み。何を話すべきか?微分方程式としては簡単なものである。運動を水平方向と鉛直方向の2方向に分けて取り扱うことに触れ,慣性の法則との関連を考えるあたりだろうか。
運動方程式
地表での物体が受ける力は,その質量に応じて
- \(\vec{F} = (0, m \, g)\)
そこから運動方程式は
- \(\begin{eqnarray} \displaystyle
m \, \frac{d^2 x}{d t^2} &=& 0\\
m \, \frac{d^2 y}{d t^2} &=& – m \, g\\
\end{eqnarray}\)
これらの式から,(4.5)式や(4.6)式で表される,速度と座標に関する式が得られるが,すでに学習済みということでここでは詳細は話さない。ただ \(x\) 方向と \(y\) 方向を独立に扱って良いことを取り上げる。
ここで,TA 作成の動画を見てもらう。動画は3つの内容が含まれる。ひとつは大きな球も小さな球も同じ速さで落下すること,二つ目は同時に二つの球を自由落下と水平方向に打ち出した場合二つの球が縦方向は同じ運動をしていること,三つ目はモンキーハンティングである。
上記動画で,自由落下と水平方向に同時に打ち出された二つの球が縦方向は同じ運動をしている。高校の頃はこのことを実験事実として扱っていたのかもしれない。水平方向に打ち出された球の初速と,同じ速度で右方向へ等速運動する観測者から見ると(細かいことはさておいて)球は鉛直に落下しているように見えるだろう。等速で運動する観測者どおしであれば,本当はどちらが運動していてどちらが静止しているのかを決める方法がなく,対等である。つまり運動する観測者と静止する観測者は同じ力学法則を観測する。それ故,両球の鉛直方向の運動は同じでなければならない。
放物運動の軌道は教科書には完全な結果の式が書かれていない。課題で,鉛直方向の最高点の座標が出て来るのもあって取り扱った。
4章 演習問題 [2]
飛行機から海上の遭難者に救助カプセルを落とす問題。500メートルの高度を時速 198km で飛行しているという条件である。
4.2 重力のもとでの運動2(空気抵抗の影響)
微分方程式を解くということを初めて扱うので,時間をかける。
最初に空気抵抗のモデルに関して話す。教科書では速度の2乗に比例する慣性抵抗を乱流の効果によるものと記述しているが,講義では流体との衝突による力積として説明する。速度 \(v\) で流体と衝突して,流体の速度がゼロから \(v\) へ変化する(これは逆に物体を静止させておいて流体を速度 \(v\) で運動していると考える方が分かりやすい。衝突によって流体の速度がゼロになると考える)。この衝突の力積は \(v\) に比例するが,衝突回数も \(v\) に比例するので,その積を考えて \(v^2\) に比例すると説明した。速度が比較的小さい場合に現れる粘性抵抗に関しては,簡単な説明をしたのみ。物体の速度が遅く流体が物体表面に沿って層状に流れ,流体中に速度差が生じるような場合の抵抗のモデルである。なぜ速度に比例するのかは私には良く分かっていないが,流体を引きずるイメージなのだろうか?速度差から摩擦のような力が想定できるが,そうすると速度に依存する摩擦力ということになる。
このあと,速度に比例する方の粘性抵抗の場合を解く。雨滴が落下する場合の運動方程式(微分方程式)を変数分離を使って解いた。
- \(\displaystyle m \, \frac{d v}{d t} = m \, g – c \, v\)
計算において\(c\) を \(m \, k\) で置き換えているが,最終的には \(k\) を使用していないので意図が良く分からない。計算は教科書のものの隙間を埋めるぐらいである。下記の雨滴の速度の式のグラフを説明して終了。
- \(\displaystyle v = \frac{m \, g}{c} \, \left( 1 – \exp \left( – \frac{c \, t}{m} \right) \right)\)
この後,変数分離の復習をやる。説明のみにとどめる。
4.3 束縛力の働く運動(束縛運動)
力学の教科書には束縛運動の話が多くある。そこには歴史的な経緯があるようだ。 力学が,微分方程式
- \(\displaystyle m \,\frac{d^2 x}{d t^2} = f_x, \quad m \, \frac{d^2 y}{d t^2} = f_y, \quad m \, \frac{d^2 z}{d t^2} = f_z\)
これらにより運動が決定されると定式化された後は,それぞれの物体間の力が万有引力のように明確であれば,問題は微分方程式が解けるかどうかだけになる。しかし物体間の力が未知である場合,つまり微分方程式を解いたのちに決定されるような場合もある。物体が複数存在する系で,それぞれの物体が相互作用するような状況(固い拘束,あるいは柔らかい拘束がある状況)が,力学の次なるターゲットになったという経緯があるようだ。
もともとが,力は物体間の拘束のようなものである。地球と太陽の運動を考えるときも,両方を一緒の系として扱えば万有引力も拘束の一種である。
束縛力があるものとして話を始めない。
運動とは力によって生じるもので,その力の方向に動き出す(本来は加速であるが)。しかし斜面の物体は力の方向に移動しない。また振り子は重力方向に運動せず円周上を運動する。こういった現象から束縛力の存在が知れる。
垂直抗力や張力などが束縛力と言われるが,名前の由来として,運動方向を限定する力であることから名づけられていて,実際は多少机がたわんだり糸が伸びて多少変形した際の復元力である。しかしその変形が微小で運動として考慮することにあまり意味が無く,その変形を無視して力のみを取り扱う。
斜面上の滑空運動と垂直抗力はパスして,単振り子と張力へ進む。
単振り子と張力
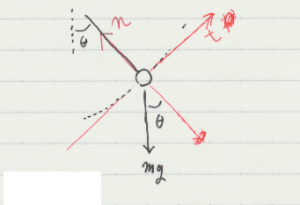
教科書では極座標を用いているとは書いていない。\(r\) 方向と反対向きに法線方向(\(n\) 方向)をとっているが,そのことは(4.42)式には影響せず符号が変わることはない。明確に極座標の例として扱う方が良いのではないか。
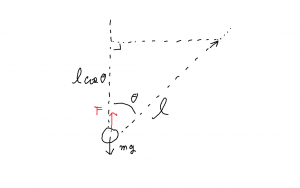
教科書では,振り子の振れ角を \(\theta\) として,錘から点Oを向いた方向(n)と振り子の軌道の方向(t)の2方向で運動方程式を組み立てる。
軌道半径を \(l\) として,方程式は下記の式となる。
- \(\begin{eqnarray} \displaystyle
m \, a_t &=& m \, l \, \frac{d^2 \theta}{d t^2} = – m \, g \sin \theta\\
m \, a_n &=& m \, l \, \left(\frac{d \theta}{d t} \right)^2 = T – m \, g \cos \theta
\end{eqnarray}\)
振り子の運動とともにn方向とt方向が変化してしまうのがいやな気がするが,これが極座標である。藤原邦男先生の『物理学序論としての力学』の87ページをみると極座標で記述している。その方程式は下記。
- \(\begin{eqnarray} \displaystyle
m \, a_r &=& m \, \left( \frac{d^2 r}{d t^2} – r \, \left( \frac{d \varphi}{d t} \right)^2 \right) = m \, g \cos \varphi – T\\
m \, a_{\varphi} &=& m \, \frac{1}{r} \, \frac{d}{d t} \, \left( r^2 \frac{d \varphi}{d t} \right) = – m \, g \sin \varphi
\end{eqnarray}\)
\(r = l\) で \(r\) が一定であるので,教科書の式と同じものに帰着する。
教科書では36ページに円運動の場合の極座標での加速度の式がある。
- \( \displaystyle
\vec{a}= – r \left(\frac{d \theta}{d t} \right)^2 \, \vec{e_{r}} + r \, \frac{d^2 \theta}{d t^2} \, \vec{e_{\theta}}
\)
このそれぞれの基本ベクトルの係数に,\(a_t\) や \(a_n\) が現れている。ここから話を始めても良いと思われる。
次に振り子の運動方程式を解く。そこで使用する \(\sin \theta \approx \theta\) の解説をした。
近似の内容を記す。ラジアンであるから半径 1 の円で角に対応する弧の長さで角度を表す。それ故,弧の長さが \(\theta\) であるが,これを \(\sin \theta\) と等しいとする近似である。これを用いるとt方向の方程式が下記となる。
- \( \displaystyle
\frac{d^2 \theta}{d t^2}= – \frac{g}{l} \, \theta\\
\)
これを解くわけだが,教科書では詳しい話をせず一般解を与えている。講義でもそれに従って微分方程式を解が満たすことを示すだけにした。
一般解は
- \( \displaystyle
\theta = A \, \cos \left( \sqrt{\frac{g}{l}} t + \delta \right)
\)
任意定数が2つ含まれるので一般解だという話は数学の授業に委ねる。
この結果を元の微分方程式に戻して,張力 \(T\)を得ることは難しい。すでに近似を使った後であり,そうなると\(\cos \theta\) の近似はどうするかが問題になる。ここでは,4章 演習問題 [6] をやってみる。状況は同じであり,これにも糸の張力が出てくる。
4章 演習問題 [6]
振り子の糸の張力 \(T\)を得るために,演習問題の[6]をとりあげる。エネルギー保存則は6章で学ぶのだが,この問題ではエネルギー保存則を使わざるを得ない。
問題は,最下点での速さを \(v_0\) として,振り子の振れ角 \(\phi\) と張力 \(T\) の関係を求めるもの。張力が現れる式としては69ページ(4.42)式があって, \(\theta\) を \(\phi\) に入れ替えて
- \(\displaystyle
m \, a_n = m \, l \, \left(\frac{d \phi}{d t} \right)^2 = T – m \, g \cos \phi .
\)
上記の \(\displaystyle \frac{d \phi}{d t} \) は角速度で,速度とは \(\displaystyle v = l \, \frac{d \phi}{d t}\) の関係にある。上式に代入して下記となる。
- \(\displaystyle
\frac{m}{l} \, v^2 = T – m \, g \cos \phi .
\)
ある振れ角 \(\phi\) での速さはエネルギー保存則で求められて,
- \(\displaystyle
v^2 = {v_0}^2 – 2 \, g \, l \, \left( 1 – \cos \phi \right) .
\)
これを利用して,振れ角と張力の関係式が求められる。
- \(\displaystyle
T = m \, \frac{{v_0}^2}{l} + m \, g \, \left( 3 \, \cos \phi – 2 \right) .
\)
この張力は近似によってられたものではなく,厳密な値である。
4.4 往復運動(単振動)
先の振り子の話と計算は重なるが,物理に詳しくない学生もいることを考慮して,とりあえず何の話か最初に明確にして始める必要はある。現実世界において,フックの法則は多く見られ,振動が単振動となる例は多いことを最初に述べる。具体的な復元力の例をばね以外もあげると良いのかもしれない。
ばねの弾力による単振動
ばねの絵を書いて座標 \(x\) の取り方や力の向きの話をして復元力とはどのようなものか話した。
- \( \displaystyle
F = – k \, x
\)
上記から運動方程式は下記のようになる。
- \( \displaystyle
m \, \frac{d^2 x}{d t^2}= – k \, x
\)
これは振り子において,振れ角が小さいとして近似をした場合と似た式である。それ故解は,下記となる。
- \( \displaystyle
x = A \, \cos \left( \omega \, t + \alpha \right)
\)
ここで \(\displaystyle \omega = \sqrt{ \frac{k}{m} }\) で,周期は下記。
- \( \displaystyle
T = 2 \, \pi \sqrt{\frac{m}{k}}
\)
振り子とは異なり,単振動では周期の式に質量が現れる。でもやはり振幅は現れない。
振幅が変わっても周期が変化しない理由の説明はやらなかった。
例題 4.3
意外な系が単振動となる例として,この例題を取りあげた。この例題を現実に再現することは可能だろうか。振動の中心は \(\displaystyle x = – \frac{l \, m}{4 \, M}\) となることも話した。
20210614 この辺りまで更新
4章 演習問題 [5]
スカイダイバーの落下運動の問題。速度の2乗に比例する慣性抵抗である。変数分離を用いる例としてやった方が良いと思う。運動方程式は下記となる。
- \(\displaystyle
m \frac{d v}{d t} = m \, g- b \, v^2 .
\)
先に,時刻無限大での終端速度を導いておく。速度が大きくなるにつれて,加速度が小さくなり,だんだんと下記の速度に近づいていく。
- \(\displaystyle
v_{\infty} = \sqrt{\frac{m \, g}{b}}.
\)
後は,変数分離で解くのみ。
- \(\displaystyle
\frac{d v}{1-\frac{b}{m \, g} \, v^2 } = g \, d t.
\)
\(\alpha = \sqrt{\frac{b}{m \, g}}\) として,左辺の分母を積の形にする。
- \(\begin{eqnarray} \displaystyle
\frac{1}{\left(1-\alpha \, v \right) \left(1+\alpha \, v \right)} \, d v &=& g \, d t\\
\frac{1}{2} \, \left\{ \frac{1}{1-\alpha \, v } + \frac{1}{1+\alpha \, v } \right\} \, d v &=& g \, d t
\end{eqnarray}\)
後は積分して下記を得る。
- \(\displaystyle
\frac{1}{2} \, \left\{-\frac{1}{\alpha} \, \log \left| 1-\alpha \, v \right| + \frac{1}{\alpha} \, \log \left| 1 + \alpha \, v \right| \right\} = g \, t + C
\)
上記を式変形し時刻ゼロで速度がゼロという条件を考慮して,下記の速度の式が得られる。
- \(\displaystyle
v = v_{\infty} \, \frac{1-\exp \left(\frac{- 2 \, g \, t}{ v_{\infty}} \right)}{1+\exp \left(\frac{- 2 \, g \, t}{ v_{\infty}} \right)}
\)
4章 演習問題 [9]
期末試験の前にやることになると思う。
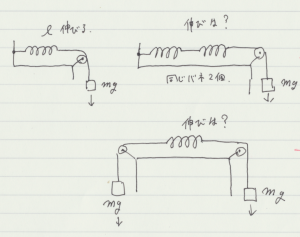
3つのばねで床と天井の間に等しい間隔で支えられている物体がある。この振動の周期を求める問題。
まず,最初にこのばねは伸びているのか縮んでいるのか気になります。これに関しては,重力を加えた力の釣り合いを考えたとき,自然長より縮んでいることはあり得ないと見て取れます。
長さ \(l\) の状態のばねの力を \(F_0\) として,物体を上方に \(\Delta x\) 動かすとします。ばねは \(\Delta x\) 縮むとき力が \(k \, \Delta x\) 減少し,伸びるとき \(k \, \Delta x\) 増加します。
もともと重力を含めた合力は釣り合っていたので,上向きを力の正方向として下記が成り立っていました。
- \(\begin{eqnarray} \displaystyle
\mathrm{合力} &=& F_0 + F_0-F_0- m \, g\\
&=& 0
\end{eqnarray}\)
物体を上方に \(\Delta x\) 動かすとき,合力はゼロではなくなり下記のように下向きの力となります。
- \(\begin{eqnarray} \displaystyle
\mathrm{合力} &=& F_0-k \, \Delta x + F_0-k \, \Delta x-\left(F_0 + k \, \Delta x \right) – m \, g\\
&=& – 3 \, k \, \Delta x.
\end{eqnarray}\)
負の力ですから,物体の移動方向とは反対向きの力が生じています。この力をひとつのばねの復元力だと見なせば振動の周期が分かります。
6章 エネルギーとその保存則
エネルギーと仕事の章。多くのテキストが仕事の定義から入る。物理では仕事というものをこのように定義する ….等の記述の後,式計算から仕事と運動エネルギーの関係を導いている。これ以外の入り方はないものか。
章のどこかで,仕事とはエネルギーの移動であることを述べるようにする。
運動の第一法則のところで,下記のような例が,ガリレオの思考実験にありました。
どのような傾斜の坂であっても,結局同じ高さまで上昇するというものでした。これを運動の法則 \(m \, \frac{d v}{d t} = F
\) を用いて考えるなら,最下点での速度から始めて,坂を上っている途中を運動方程式で追いかけて速度変化を求めていって,速度がゼロとなったところを比べるとすべて同じ高さになるというわけです。しかしながらこれ等のことは,何か別の包括的な法則がそこに隠れていることを示唆しているようにも思えます。
運動をどのような量で測るのかということが,以前議論されたことがありました。\(m \, v\) で表すべきだとするデカルト派と,\(m \, v^2\) で表すべきだというライプニッツ派が激しく議論を闘わせました。デカルト派は衝突現象などから,保存される量としての \(m \, v\) を重要な量だと考えました。ライプニッツ派は落下運動を根拠とします。落下は運動を生み出すわけだから,運動は高さによって測ることができると考えました。4倍の高さから落下する時,得られる速度は元の2倍に過ぎません。それ故,速度の2乗が運動を測る量としては適当であると主張します。
この議論は,方や運動量保存則,方やエネルギー保存則ということで,どちらが間違いということではなかったわけですが,結局ダランベールによってこの議論は決着します。私には良く分かっていないところもあるのですが,書いてみると,4倍の高さから落下する時,落下にかかる時間は元の時間の2倍です。つまり重力が物体に加わっている時間は2倍の時間です。運動を力が加わった時間で評価すると,この場合は投げ上げる場合を考えた方が分かりやすいですが,投げ上げるとき速度がゼロになるまでにかかる時間は,初速を2倍にすると2倍になります。重力が2倍の時間加わることで速度を完全に失います。つまり運動を力が加わった時間で評価すると,速度が2倍であるなら“運動の量”は2倍となります。これを力が加わった距離で評価すると,初速が2倍なら物体は元の4倍の高さまで上昇するわけですから,“運動の量”は4倍になります。このように,力を加えた時間で評価するか,加えた距離で評価するかによる違いであるとダランベールは結論します。
力を加えた時間に応じた運動の変化とは,力積に対応した現在の意味の“運動量”の変化の話ですが,下記のような積分計算で示されます。
- \(\begin{eqnarray} \displaystyle
\int_{t_1}^{t_2} m \, \frac{d v}{d t} dt &=& \int_{t_1}^{t_2} F dt\\
m \, v_2- m \, v_1 &=& \int_{t_1}^{t_2} F dt.
\end{eqnarray}\)
力を加えた(力が作用した)距離による運動の変化とは, \(m \, \frac{d v}{d t} = F\) を座標で積分することになりそうで,その右辺は下記のような式となって,
- \(\displaystyle
\int F d x
\)
これは仕事といわれる量です。運動方程式の左辺の積分は,結局運動エネルギーとなるわけですが,その辺の話はこの章の(6.5)でやります。
6.1 仕事
以下,中学,高校で既に仕事という概念を学習済みであるということが前提になっている説明。もっと根本からの話をやりたいところ。
以下,仕事の例をあげて,その定義の復習をやっていきます。
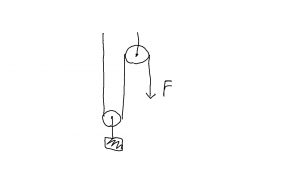
力と作用した距離の積は,滑車の話で出てきます。上図のように滑車を組み合わせると,持ち上げる力は半分になりますがひもを引く距離は倍になります。それでは楽になったとは言えない。『マッハ力学』(p45)では,このことを,機械を使って仕事を節約することはできないと表現していて,力と距離の積が重要であることが,このような現象から理解されて来たのだと思います。講義では,積が重要なのだから,積の値が同じであることに意味がある(何らかの等価性を示している)という点を協調すべきと思う。
もう一つの例をあげます。初期の蒸気エンジンの性能を示すのに,時間あたりどれぐらいの水を汲み上げるのかという指標がありました。1 分間で 3300 ポンドを1 フィート持ち上げるとかです(1 馬力)。時間あたりなので仕事率に相当するものですが,1 分間という枠をはずせば,物理の中での仕事の概念とぴったりです。
この章ではエネルギーという概念も出てくるのですが,エネルギーという言葉は,蒸気エンジンが登場して後の言葉です。もちろん \(m \, v^2\) が運動を表す上で重要であることは,デカルトやライプニッツの頃から意識されていました。ただあてはまる名称が無かったということは,動力を作り出すエンジンが登場するまで,その意識は力学の中にとどまっていたということかと思います。
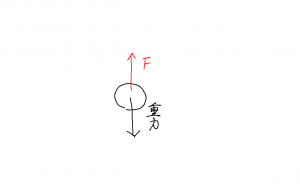
教科書の解説は,何かの力に逆らって物体を移動させるという話ではないのですが,以下では重力に逆らって水を汲み上げるということを例として,仕事について考えてみましょう。図のように(水を単純な丸い物体として書きました),重力に逆らって持ち上げるなら,必要な力は重力と同じ大きさで反対向きとなります。それで十分です。後は定速でゆっくりと移動すると考えます。つまり力が釣り合っている状態で持ち上げます。
移動する方向は重要です。力が釣り合っているので自由にどの方向にも移動できます。しかし水平に移動しても水を汲み上げたことにはなりません。重力と逆の方向に移動した距離が重要です。図に示すように \(l\) 移動したとしても重力と逆方向に移動した距離 \(l \, \cos \theta\) が有効な仕事(持ち上げた高さ)です。これが距離に \(\cos \theta\) をかける理由です。この仕事は \(F \, l \, \cos \theta\) となります。
釣り合いの状態意外で移動させることも考えられますが,その時は物体に運動エネルギーの増加ももたらします。
先ほどの仕事 \(F \, l \, \cos \theta\) は,ベクトルの内積を使って表せます。移動を \(\vec{l}\) として,仕事は
- \(\begin{eqnarray} \displaystyle
\mathrm{仕事} &=& F \, l \, \cos \theta\\
&=& \vec{F} \cdot \vec{l}
\end{eqnarray}\)
仕事の定義の復習はここで終わり。
変化する力による仕事-ばねを引き伸ばすための仕事
一定の力ではなく強さが変化する場合の仕事の求め方。ばねを例として取り上げる。結果を学生は知っているだけに興味を持たせることが難しく思える。
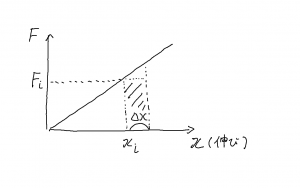
力-変位のグラフを示し,微小変位 \(\Delta x\) 伸ばした場合の仕事 \(\Delta W_i\)
- \(\displaystyle
\Delta W_i = F_i \, \Delta x
\)
上記は下のグラフの短冊の面積に相当する。
そのため,自然長から \(x\) までばねを伸ばすときに \(F\) がする仕事 \(W\) は
- \(\begin{eqnarray} \displaystyle
W &=& \sum_{i} F_i \, \Delta x\\
W &=& \sum_{i} k \, x_i \, \Delta x
\end{eqnarray}\)
\(\Delta x\) を小さくすることで,上記の和を積分に置き換える。
- \(\begin{eqnarray} \displaystyle
W &=& \int_{0}^{x} k \, x’ \, dx’\\
W &=& \frac{1}{2} k \, x^2
\end{eqnarray}\)
結局,力-変位のグラフの面積を求めたことを協調した。それは学生はすでに知っていることかもしれないが,次の「6.2 仕事の一般的定義」で仕事の計算に線積分を使うので,積分との関連を強調した方が良いと思う。それだけが目的かも。
6.2 仕事の一般的定義
仕事の計算を直線上だけでなく,それ以外の自由な曲線上の経路で考える。移動経路を微小な部分に分割して,それぞれの微小変位での仕事を計算しその和を求める。なぜ仕事がスカラーとして足し算可能なものであるのかという理由は説明しない。仕事とエネルギーの関連はまだ出てきていないので,足し算をどのように学生はイメージするのだろうか。先のばねを伸ばすときの仕事の計算でも微小仕事の和を考えた。直線上ではあまり気にならなかったが,曲線上で和を考えるとき,仕事がスカラーでありその和にも意味があることを,暗黙のうちに仮定していることが気になる。これを解消する始め方というのがあるのか。
教科書では一般的な話として,任意の曲線に沿って移動する場合の仕事の定義を与えている。とりあえず最初は教科書の入りを読んで計算方法の大まかなところをみた後,具体的に万有引力のもとでの移動の話として説明してみた。そこに違いはないのかもしれないが,具体的な話の方が取り扱わなければならない必然性はあるように学生は感じるのではないか。
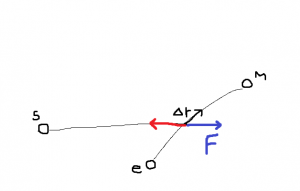
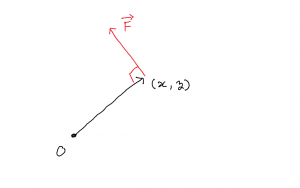
太陽(S)の引力に逆らって地球(e)から火星(M)まで移動する。上図の \(\Delta r\) 移動するときの仕事は,引力(赤)と反対向きで同じ大きさの力を \(\vec{F}\) として
- \(\displaystyle
\Delta W_i = \vec{F}(\vec{r}_i) \cdot \Delta \vec{r}_i
\)
全体の仕事 \(W\) は
- \(\begin{eqnarray} \displaystyle
W &=& \sum_i \Delta W_i\\
&=& \sum_i \vec{F}(\vec{r}_i) \cdot \Delta \vec{r}_i
\end{eqnarray}\)
\(\Delta r_i\) を小さくして
- \(\displaystyle
W = \int_{\mathrm{地球}}^{\mathrm{火星}} \vec{F}(\vec{r}) \cdot d \vec{r}
\)
学生はまだ線積分を習っていないので,積分を成分ごとの計算に分ける。
- \(\displaystyle
W = \int F_x \, d x + \int F_y \, d y + \int F_z \, d z
\)
上記なら計算できる。この分けた積分の計算が次の「重力がする仕事」につながる。
重力がする仕事
ここは教科書の記述とほぼ同ように話す。スキーヤーが雪の斜面を高さ \(h\) 滑り降りるときに重力がする仕事を求める話。先の記述にあった仕事を求める線積分を具体的に計算する例。今まで,重力に逆らって移動させる仕事を考えてきたが,ここでは重力がする仕事を求めるので話が反対になっている。学生は戸惑わなかったのだろうか。
力と変位のベクトルの記法は教科書から少し変える。
- \(\displaystyle
\vec{F}(\vec{r}) = ( 0, – m \, g), \quad d \vec{r} = (d x, d y)
\)
全体の仕事は
- \(\begin{eqnarray} \displaystyle
W &=& \int \vec{F}(\vec{r}) \cdot d \vec{r}\\
&=& \int F_x \, d x + \int F_y \, d y\\
&=& \int_{h}^{0} – m \, g \, dy\\
&=& m \, g \, h
\end{eqnarray}\)
斜面の形が計算には全く出てこなかったことから,経路に依らない値であることを強調した。この後の保存力の話への伏線のつもり。
仕事率
よく考えたら,まだ仕事の単位(ジュール)のことを話していなかった。ここに盛り込もう。
ここは簡単に,ワットの話でもすれば良いのではないかと思う。ただし,力学における仕事率は力と速度の積なのだが,教科書は仕事を時間で割った計算を示しているだけで,瞬間の計算をきちんとすればその記述は間違いではないのだが,幾分注意が必要かもしれない。
単位時間あたりの仕事について考える。講義ではこれから出てくる話だが,仕事はエネルギーに変わり,それゆえ単位時間あたりの仕事は単位時間あたりのエネルギーの送出や消費の話につながる。
\(\Delta t\) の間に \(\Delta W\) の仕事をするとして,仕事率 \(P_{AV}\) は
- \(\displaystyle
P_{AV} = \frac{\Delta W}{\Delta t}
\)
力学では, \(\Delta t\) で \(\Delta \ell\) 移動する場合,速度を \(v\) として
- \(\begin{eqnarray} \displaystyle
\Delta W &=& F \, \Delta \ell\\
&=& F \, v \, \Delta t.
\end{eqnarray}\)
それゆえ,仕事率 \(P\) は
- \(\begin{eqnarray} \displaystyle
P &=& \frac{\Delta W}{\Delta t}\\
&=& \frac{F \, v \, \Delta t}{\Delta t}\\
&=& F \, v.
\end{eqnarray}\)
これからすると一定の力を加え続ける等加速度運動でも,速度の増加と共に仕事率は増加している。最終的な運動エネルギーを加速に要した時間で割っても仕事率は得られない。
上の計算で力が作用した距離を考える際に速度と微小時間の積を考えたが,これはこの後の運動方程式の積分を考えるときに似たようなことをやるので,その前振りになるかも。
6.4 保存力と位置エネルギー
例題 6.1 を先に挟むかどうか悩むところだけど,今回は挟まない。ここは具体的な例から入りたい。保存力となる具体的な例から入りたい。それにしても,なぜ保存力をここで持ち出してくるのか,いつものことながらその理由付けが難しい。理由付けは要らないのだろうか。本を読んでいるときは確かにあまり理由付けは要らないような気がするが,いざ講義で話し始めると,なぜこの話をするのかという理由が欠けていると非常にやりにくい。
先に,重力がする仕事は高さの差のみで決まり経路に依らないというのがあった。逆に重力に逆らって持ち上げるときも,斜面との摩擦が無視できるのであれば必要な仕事は経路に依らない。万有引力もまた同様である。下図のように,星 M からの引力により P1 から P2 まで移動するときに,万有引力がする仕事を考える。
移動する経路のうち,ふたつの同心円を横切る区間 \(\Delta \vec{s}\) での仕事 \(\Delta W\) は
- \(\begin{eqnarray} \displaystyle
\Delta W &=& \vec{F} \cdot \Delta \vec{s}\\
&=& \left|\vec{F}\right| \cdot \left|\Delta \vec{s}\right| \, \cos \theta\\
&=& \left|\vec{F}\right| \, \Delta r.
\end{eqnarray}\)
このふたつの同心円をどのように横切ろうと仕事は変わらない。加えて同心円の円周に沿って移動するときは \(\theta = 90^{\circ}\) なので仕事はゼロである。それゆえどの経路を通ろうと万有引力のする仕事は同じ値になる。また逆に引力に逆らって移動する場合も同様に必要な仕事は経路に依らない。このように仕事が経路に依らない力を保存力という。
保存力という名前はいかにも何か保存される量と関わりがあるのだろうという感じがしますが,仕事を求めた計算の積分範囲の始点(以下では \(\vec{r_0}\) )を固定すれば,座標だけで決定されるスカラー関数 \(U \left( \vec{r} \right)\) が考えられます。
- \(\begin{eqnarray} \displaystyle
W \left( \vec{r}, \vec{r}_0 \right) &=& – \int_{\vec{r}_0}^{\vec{r}} \vec{F} \cdot d \vec{r}\\
U \left( \vec{r} \right) &=& – \int_{\vec{r}_0}^{\vec{r}} \vec{F} \cdot d \vec{r}.
\end{eqnarray}\)
\(U \left( \vec{r} \right)\) は位置エネルギーやポテンシャルエネルギーなどと言われる量です。またこの保存力のもとで,任意の2点間を移動するときに必要な仕事を \(U \left( \vec{r} \right)\) を用いて表してみます。
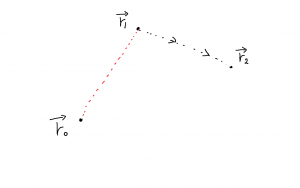
どの経路で仕事を計算しても同じ値になるのだから, \(\vec{r}_0\) から出発して \(\vec{r}_1\) を経由し \(\vec{r}_2\) に至る経路で仕事を計算します。
- \(\begin{eqnarray} \displaystyle
W \left( \vec{r}_2, \vec{r}_1 \right) &=& – \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d \vec{r}\\
W \left( \vec{r}_2, \vec{r}_0 \right) – W \left( \vec{r}_1, \vec{r}_0 \right)&=& – \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d \vec{r}\\
U \left( \vec{r}_2 \right) – U \left( \vec{r}_1 \right)&=& – \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d \vec{r}
\end{eqnarray}\)
この式はこの後のエネルギー保存のところで使います。
6.5 運動方程式のエネルギー積分
6 章の始めから仕事に関して考えてきて,ここでやっと運動と仕事が結びつきます。運動方程式は
- \(\displaystyle
m \frac{d \vec{v}}{d t} = \vec{F}
\)
上記のように微分の式なのですが,微分する前の形が存在するのか。また仕事は運動方程式の右辺を座標で積分した形をしています。
- \(\displaystyle
\int \vec{F} \cdot d \vec{r}
\)
左辺を座標で積分するとどうなるのか,というのがここの内容です。
1次元の運動
最初は 1 次元で考えましょう。力は座標で決まるものを想定します。一次元なので運動方程式は下記。
- \(\displaystyle
m \frac{d v}{d t} = F(x).
\)
仕事は右辺を座標で積分したものなので,両辺を座標で積分してみます。
- \(\displaystyle
\int m \frac{d v}{d t} \, d x = \int F(x) \, d x.
\)
右辺は仕事そのものなのでほっといて,左辺を計算してみます。まずは積分の変数変換。
- \(\begin{eqnarray} \displaystyle
d x &=& \frac{d x}{d t} \, d t\\
&=& v \, d t
\end{eqnarray}\)
これを用いて左辺を計算すると
- \(\begin{eqnarray} \displaystyle
\mathrm{左辺} &=& \int m \, \frac{d v}{d t} \, v \, d t\\
&=& \frac{m}{2} \, \int_{t_1}^{t_2} \frac{d}{d t} \left( v^2 \right) \, d t\\
&=& \frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2}
\end{eqnarray}\)
\(v_1\) , \(v_2\) は時刻 \(t_1\) , \(t_2\) での速度です。右辺と合わせると下記。
- \(\displaystyle
\frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2} = \int_{x_1}^{x_2} F(x) \, d x.
\)
( 仕事が正の値ならば)仕事を加えることで \(\displaystyle \frac{1}{2} \, m \, v^{2}\) が増加しています。これが仕事と運動の関係です。やっと落ちが付きました。
\(F(x)\) が保存力であるとして,下記のようにポテンシャルエネルギーを定義します。
- \(\displaystyle
U \left( x \right) = – \int_{x_0}^{x} F(x’) \, d x’.
\)
先ほどの右辺の仕事を,この \(U(x)\) を用いて表すと
- \(\begin{eqnarray} \displaystyle
\int_{x_1}^{x_2} F(x) \, d x &=& \int_{x_0}^{x_2} F(x) \, d x-\int_{x_0}^{x_1} F(x) \, d x\\
&=& – U(x_{2}) + U(x_{1}).
\end{eqnarray}\)
上記で右辺を置き換えると,結局
- \(\begin{eqnarray} \displaystyle
\frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2} &=& – U(x_{2}) + U(x_{1})\\
\frac{1}{2} \, m \, v_{2}^{2} + U(x_{2}) &=& \frac{1}{2} \, m \, v_{1}^{2} + U(x_{1})
\end{eqnarray}\)
保存力による運動では,\(\displaystyle \frac{1}{2} \, m \, v^{2} + U(x)\) が一定の値となっています。それでこの一定の値として保持されている何かにエネルギーという名が付きました。
運動エネルギー
ここは先ほどの仕事と運動の関係を 3 次元にしただけです。
下記の運動方程式の両辺を上図の経路に沿って座標で積分することを考えます。
- \(\displaystyle
m \frac{d \vec{v}}{d t} = \vec{F}
\)
右辺の積分は仕事そのものです。
- \(\displaystyle
\int \vec{F} \cdot d \vec{r}
\)
ここで \(d \vec{r} = (d x, d y, d z)\) です。続いて左辺の積分を考えてみましょう。
- \(\begin{eqnarray} \displaystyle
\mathrm{左辺} &=& \int m \, \frac{d \vec{v}}{d t} \cdot d \vec{r}\\
&=& \int m \, \frac{d v_x}{d t} \, d x + \int m \, \frac{d v_y}{d t} \, d y + \int m \, \frac{d v_z}{d t} \, d z
\end{eqnarray}\)
ここで項のひとつだけを取り出してみます。
- \(\begin{eqnarray} \displaystyle
\int m \, \frac{d v_x}{d t} \, d x &=& \int m \, \frac{d v_x}{d t} \, v_x \, d t\\
&=& \frac{m}{2} \, \int_{t_1}^{t_2} \frac{d}{d t} \left( v_{x}^2 \right) \, d t\\
&=& \frac{1}{2} \, m \, v_{x}^{2}(t_2)- \frac{1}{2} \, m \, v_{x}^{2}(t_1)
\end{eqnarray}\)
よって左辺は
- \(\displaystyle
\mathrm{左辺} = \frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2}
\)
右辺と繋ぎます。 \(\vec{F}\) が保存力であるとして,そのポテンシャルエネルギーを \(U\) とすれば,
- \(\begin{eqnarray} \displaystyle
\frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2} &=& \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d \vec{r}\\
\frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2} &=& – U \left( \vec{r}_2\right) + U \left( \vec{r}_1\right)\\
\frac{1}{2} \, m \, v_{2}^{2} + U \left( \vec{r}_2\right) &=& \frac{1}{2} \, m \, v_{1}^{2} + U \left( \vec{r}_1\right)
\end{eqnarray}\)
1 次元と同じようにエネルギー保存則が成立しました。
例題 6.1
さて,仕事の計算です。慣れない線積分をやってみるという例題ですが,結局成分に分けて計算してしまうので通常の積分とあまり変わりがありません。
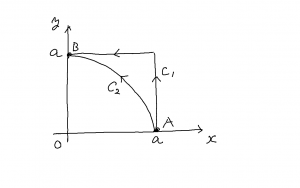
質量 \(m\) の物体が,力 \(\vec{F} = (-k\, y, k \, x)\) を受けて,下図のような平面上を点 A から点 B まで移動します。変数 \(k\) を付けているのは次元(単位)を考えてのことだと思います。
C1の経路(正方形の辺上)とC2(円周上)で仕事を計算します。力がどんな感じのものなのか少し考えてみます。位置ベクトルと力の式から,両者が直交していることが分かります。
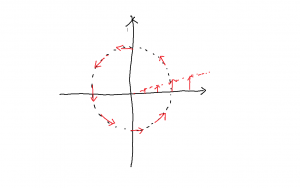
円周上では(半径 \(r\) ),力は大きさが一定で,接線方向に向いています。 \(r\) が大きくなるにつれて,力も大きくなります。
- \(\begin{eqnarray} \displaystyle
\vec{F} &=& \sqrt{k^2 \, x^2 + k^2 \, y^2}\\
&=& k \, r
\end{eqnarray}\)
そのため,力は下図の様に渦を巻いています。原点から遠ざかるほど力は大きくなります。
まずは C1 に沿って,仕事を計算してみましょう。C1 上で \(\displaystyle \int \vec{F} \cdot d \vec{r}\) を求めます。 \(d \vec{r} = (d x, d y)\) として,\(\vec{F}\) との内積を考えます。
- \(\begin{eqnarray} \displaystyle
\int_{C_1} \vec{F} \cdot d \vec{r} &=& \int_{C_1} F_x \, d x + \int_{C_1} F_y \, d y\\
&=& \int_{a}^{0} – k \, a \, d x + \int_{0}^{a} k \, a \, d y\\
&=& – k \, a \, \Bigl[\, x \, \Bigr]_{a}^{0} + k \, a \, \Bigl[\, y \, \Bigr]_{0}^{a}\\
&=& 2 \, k \, a^2
\end{eqnarray}\)
次に C2 上で計算してみましょう。変数変換をしたいのですが, \(\vec{r} = ( x, y) = (a \, \cos \theta, a \, \sin \theta)\) として,
- \(\begin{eqnarray} \displaystyle
d \vec{r} &=& ( d x, d y)\\
&=& ( -a \, \sin \theta \, d \theta, a \, \cos \theta \, d \theta)
\end{eqnarray}\)
また力は
- \(\begin{eqnarray} \displaystyle
\vec{F} &=& ( – k \, y, k \, x)\\
&=& ( -k \, a \, \sin \theta, k \, a \, \cos \theta)
\end{eqnarray}\)
よって
- \(\begin{eqnarray} \displaystyle
\vec{F} \cdot d \vec{r} &=& k \, a^2 \, \sin^2 \theta \, d \theta + k \, a^2 \, \cos^2 \theta \, d \theta\\
&=& k \, a^2 \, d \theta
\end{eqnarray}\)
上記を使って仕事を計算します。
- \(\begin{eqnarray} \displaystyle
\int_{C_2} \vec{F} \cdot d \vec{r} &=& \int_{0}^{\frac{\pi}{2}} k \, a^2 \, d \theta\\
&=& k \, a^2 \, \Bigl[ \, \theta \, \Bigr]_{0}^{\frac{\pi}{2}}\\
&=& \frac{\pi}{2} \, k \, a^2
\end{eqnarray}\)
C3 もあったのですがパスします。さて,上記二通りの計算から,経路によって仕事の値が異なる結果となりました。それゆえこの力は保存力ではありません。保存力は位置エネルギーと関連した力です。位置エネルギーの勾配として,坂を下る方向に力が定義されます。それゆえ力に相当する勾配を与える等高線が考えられないと保存力ではありません。この例題の力は渦を巻いていました。渦巻き状の力を与える等高線を引くことは不可能ですね。
例題 6.3
計算が大変ですが,これをやります。いつものことながら計算だけで講義中に時間がかなりかかりそう。計算を講義中にやることは意味があるのかとよく考えますが,計算しないと説得力が無いような気がして,やはりやることになります。どう考えるべきか。
問題は,力学的エネルギー保存則の式を変形して,次の関係式を導け,というものです。
- 重力のもとで鉛直方向に運動する物体の高さ \(z(t)\)
\(\displaystyle z(t) = z_0 \pm v_{0} \, t-\frac{1}{2} \, g \, t^2\) - 長さ \(\ell\) の糸におもりを付けた単振り子の運動方程式
\(\displaystyle \frac{d^2 \theta}{d t^2} = – \frac{g}{\ell} \, \sin \theta\)
1. は下記の式から始めて
- \(\displaystyle
\frac{1}{2} \, m \, \left( \frac{d z}{d t} \right)^2 + m \, g \, z = \frac{1}{2} \, m \, v_{0}^2 + m \, g \, z_0
\)
\(z(t) = . . .\) の形に変形していきます。途中で変数分離を使います。計算は教科書のままなので此処に書きません。
2. は下記の式から始めて
- \(\displaystyle
\frac{1}{2} \, m \, \left( \ell \, \frac{d \theta}{d t} \right)^2 + m \, g \, \ell \, \left( 1-\cos \theta \right) = \mathrm{一定}
\)
上記の両辺を時間で微分します。これも計算がほぼ教科書のままなので此処に書きません。
ただ授業ではエネルギー保存則を時間で微分したら運動方程式になったことを強調したい。例題の解答とは別に 1. のエネルギー保存則の式を時間で微分することをやってみます。再掲ですが
- \(\displaystyle
\frac{1}{2} \, m \, \left( \frac{d z}{d t} \right)^2 + m \, g \, z = \frac{1}{2} \, m \, v_{0}^2 + m \, g \, z_0
\)
上記の両辺を時間で微分します。
- \(\begin{eqnarray} \displaystyle
m \, \left( \frac{d z}{d t} \right) \, \frac{d^2 z}{d t^2} + m \, g \, \frac{d z}{d t} &=& 0\\
m \, \frac{d^2 z}{d t^2} &=& – m \, g
\end{eqnarray}\)
こちらも微分することで運動方程式が得られました。6 章の最初で話した,運動方程式の元となる式としてエネルギー保存則の式が挙げられるということで落ちを付けたい。
だいたいこのあたりで講義は終了かと思います。後は演習と期末試験だけ。最後の日に(不吉な)再試の話を忘れない。再試用の演習問題を期末試験終了後に Moodle にアップすることを連絡する。