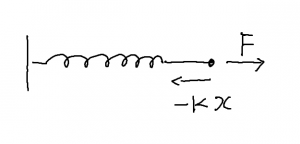2019 力学

　力学の授業です。教科書は，永田一清著『新基礎力学』サイエンス社です。

　このうち，第ゼロ章「はじめに」，第1章「運動の表し方（１）」，第2章「運動の表し方（２）」，第3章「力と運動」，第4章「いろいろな運動（１）」，第6章「エネルギーとその保存則」が講義で取り扱う範囲です。

　中間テスト，期末テスト，e-Learning の課題で成績を評価します。以下，講義の内容や反省点等を書いてみます。当分は未完成の内容とお考えください。

０章 はじめに

　ここはほぼ省略した。力学の歴史が主な内容である。アリストテレスの運動に関する理解や，その後のニュートンの話である。「運動の３法則」のイントロとしては必要な内容であるが，どちらかと言えばこの内容は所々で話に織り込んでいった方が良いかなと思う。

１章 運動の表し方（１）

　運動学といわれる領域。運動の記述である。

1.1 位置と座標系

　直交座標系や右手系のことが記述されている。日頃使用しているままで，新たに再認識する必要はないと思うので，あまり内容に触れることなく，ただ座標を時間の関数として \(x(t)\) と表すことだけ話す。\( x = f(t)\) ではなくて \(x = x(t)\) という感じで，\(f\) のような名前を持ち出すことなく表記することに慣れてもらいたいということだけ話した。

1.2 ２次元極座標と弧度法

　極座標は，この後の講義でそれほど出てくるわけではないが，ラジアンの定義や利用方法を思い出してもらいたいので，簡単に定義を確認した後，例題 1.1 に飛ぶ。

例題 1.1

　等速円運動の速度 \(v\) を角速度に変換する所でラジアンの定義を再度確認することが要点。

1.3 位置ベクトルと変位ベクトル

　ベクトルとスカラーの話である。ベクトルとは何かを話す必要はないと思う。

1.4 ベクトルの基本的性質

　ベクトルの和と差，成分表示など。ここも特に取り扱う必要はないと思う。章末の演習問題をやるのみで良いと思う。

第１章演習問題

　[5] のみを取り扱った。

e-learning による課題の準備

　e-learning で宿題をだすので，その利用方法の説明。パソコン教室ではないが携帯で Wi-Fi につないでもらって，実際に解答する（下図）。

数式の入力方法と入力例を見せること，採点が今日は自動採点であるが，実際の課題は後採点で「accepted」とだけ表示されること等を話す。

　このあたりで初日の終わり。時間的に余裕があるなら「力学概念調査」をやってみるというのもあるかも。

２章 運動の表し方（２）

　前章の運動学の続き。前章は座標を取り扱ったが，ここでは速度，加速度を取り扱う。ただし力は取り扱わないことに注意する。放物運動も演習問題にはあるが，力との絡みはない。

2.1 速さ

　速さに関しては瞬間の速さの定義に微分を持ち出すところが中心です。速度が距離の時間微分で得られることは高校の頃聞いたことがあるかもしれませんが，ここで有無を言わさず微分を導入します。この後逆に速さから距離を得る場合の積分にいく前に演習を入れます。

e-learning 練習問題01

よくある問題ですが，速度－時間のグラフの面積から移動距離を導く問題。どこからかとってきた問題だったと . . .

解答欄が図に入りきっていません。ここで面積から移動距離を導く話を復習しておいて，次の速度－時間のグラフを積分する話につなげます。

\(\displaystyle s = \int_{t_A}^{t_B} v(x) dt\)

2.2 速度

　ベクトル的な速さの取り扱い方です。とくにその点は問題にならないと思います。先の 2.1 でやった移動距離の時間微分の話がどうなるのかという所の説明ぐらいかと思います。

\(\begin{eqnarray} \displaystyle
\vec{v} &=& \frac{d \vec{r}}{d t} \\
&=& \left( \frac{d x}{d t} , \, \frac{d y}{d t} \right)
\end{eqnarray} \)

それぞれの成分の微分になるというところぐらいを話せば良いかなと思っています。

2.3 加速度

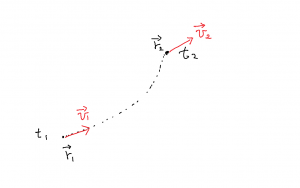
　教科書では，加速度はいきなりベクトル的に取り扱います。前振りとしての直線運動の加速度の話はないですね。ここでは時刻 \(t\) から \(t + \Delta t\) 間の速度の変化 \(\Delta \vec{v} = \vec{v}(t + \Delta t) – \vec{v} (t)\) を考えるときに，それぞれの速度ベクトルの始点を揃えて配置するというところを話します。後は加速度が速度の微分であることを話します。

\(\displaystyle \vec{a} = \left( \frac{d v_x}{d t} , \, \frac{d v_y}{d t} \right)\)

2.4 等加速度運動

　ここになぜ等加速度運動の話が来るのか最初は良く分からなかったのですが，先で座標，速度，加速度が微分や積分で関係していることを話していて，でも具体的には何もとり扱っていません。そこで例として加速度が一定となる場合に微積の関係がどうなるのか見てみるという位置づけなのかと思います（当たり前！）。教科書では，加速度から速度を求めて次に座標という順に，積分していく方向で取り扱っています。導かれる結果が高校ですでに学習済みである点は気になりますが（パスするべきか？），微積の関係を確認しておいた方が良いのかもしれません。

このあたりで2日目の終わり。

(2.5)　等速円運動

内容は等速円運動を例として，先週話をした加速度の定義等を考えてみるという位置づけだと思います。

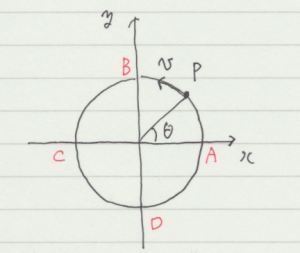
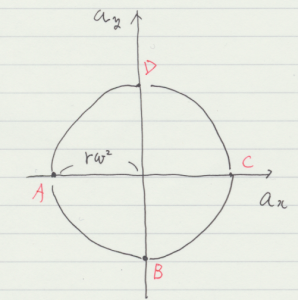
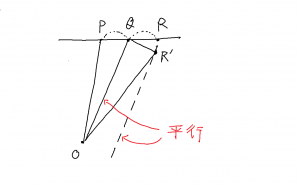
下図のように，半径 \(r\) の円周上を点 P が速度 \(v\) で運動しています。

fig. 2.5.1

図中の\(\theta\) は時間に対して一定の割合で増加しますが，この増加分（角速度）を \(\omega\) とします。 \(r\)，\(\theta\)，\(\omega\) の間には \( v = r \, \omega\) が成り立ちます。以下，円運動の速度と加速度に関して考えてみます。

fig. 2.5.2

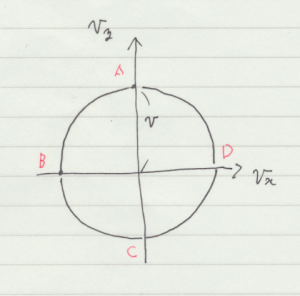
高校で円運動を学ぶときにはあまり使いませんが，ホドグラフという図（上図）を利用します。速度を座標としてプロットしたものです。fig. 2.5.1 で \(x\) 軸上の点 A に質点があるとき，その速度は fig. 2.5.2 上で， \(y\) 軸上にあります。この図を使って，点 A での加速度を考えます。

fig. 2.5.3

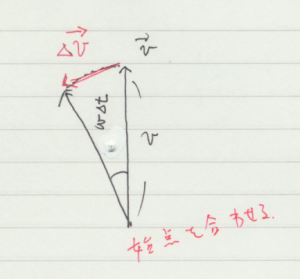
質点が点 A の位置にあるときから \(\Delta t\) 秒経過した時刻の速度変化を考えます。点 A の時刻において，ホドグラフ上で \(y\) 軸方向を向いていた速度は左側に倒れ，\(\omega \Delta t\) 回転しています。この速度変化 \(\vec{\Delta v}\) は，大きさが \(| \vec{\Delta v} | = r \, {\omega}^2 \, \Delta t\) です。それゆえ加速度 \(\vec{a}\) の大きさは

\(\begin{eqnarray} \displaystyle | \vec{a} | &=& \frac{| \vec{\Delta v} |}{\Delta t} \\ &=& r \, {\omega}^2 . \end{eqnarray}\)

その向きは，水平方向左向きですが， fig. 2.5.1 に戻って考えると，円運動の中心を向いています。前の週に，速度変化を考えるとき速度ベクトルの始点を揃えて比較するという話がありましたが，ホドグラフを使うと自動的に始点を揃えて考えています。加速度のグラフを fig. 2.5.3 に示します。

fig. 2.5.3

例題 2.2

　円運動とのつながりから，例題 2.1 をとばして例題 2.2 を扱います。この例題は極座標における基本ベクトルを考えるものです。

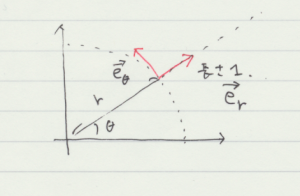
質点が上図のように原点からの距離 \(r\) で，\(x\) 軸との角度 \(\theta\) にあるとき，その基本ベクトル \(\vec{e_{r}}\) と \(\vec{e_{\theta}}\) は

\(\begin{eqnarray} \displaystyle \vec{e_{r}} &=& \left( \cos \theta , \, \sin \theta \right) \\ \vec{e_{\theta}} &=& \left( – \sin \theta , \, \cos \theta \right) . \end{eqnarray}\)

このベクトルは点がどこにあるかによって異なるものとなります。それゆえ質点が運動する場合などは時間変化するということで，教科書では問題(1)として， \(\vec{e_{r}}\) と \(\vec{e_{\theta}}\) の時間変化を求めます。

\(\begin{eqnarray} \displaystyle
\frac{d \vec{e_{r}}}{d t} &=& \left( \frac{d \cos \theta}{d t} , \, \frac{d \sin \theta}{d t} \right) \\
&=& \left( – \sin \theta \, \frac{d \theta}{d t} , \, \cos \theta \, \frac{d \theta}{d t} \right) \\
&=& \frac{d \theta}{d t} \, \left( – \sin \theta , \, \cos \theta \right) \\
&=& \frac{d \theta}{d t} \, \vec{e_{\theta}}
\end{eqnarray}\)

また同様にして

\(\begin{eqnarray} \displaystyle
\frac{d \vec{e_{\theta}}}{d t} = – \frac{d \theta}{d t} \, \vec{e_{r}} . \\
\end{eqnarray}\)

基本ベクトルの時間変化とは何か？いまひとつピンとこないところもありますが，次の問題(2)では円運動の場合の速度ベクトルや加速度ベクトルを求めるという展開です。以下では，教科書とは異なるのですが，円運動に限定せず極座標における速度ベクトルを考えてみます。

　極座標における位置ベクトル \(\vec{r}\) は，\(\vec{r} = r \, \vec{e_{r}}\) と表されるので，これを時間微分して速度を求めます。

\(\begin{eqnarray} \displaystyle
\vec{v} &=& \frac{d \vec{r}}{d t} \\
&=& \frac{d r}{d t} \, \vec{e_{r}} + r \, \frac{d \vec{e_{r}}}{d t}\\
&=& \frac{d r}{d t} \, \vec{e_{r}} + r \, \frac{d \theta}{d t} \, \vec{e_{\theta}}
\end{eqnarray}\)

上記の様に，極座標で速度を考えるとすぐに基本ベクトルの時間微分が出てきました。加速度を考えると \(\vec{e_{\theta}}\) の時間微分も出てきます。こんなところが基本ベクトルの時間変化を考える理由でしょうか。

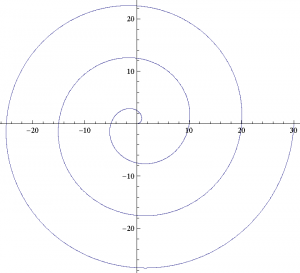
演習問題 [6] の(3)

続けてやるなら極座標の例題だと思って，この演習問題 [6] の(3)を次に取り扱いました。螺旋運動の軌道，速度，加速度を求める問題です。座標は以下の様な式で表されます。

\(\begin{eqnarray} \displaystyle
x &=& v_0 \, t \cos \omega \, t \\
y &=& v_0 \, t \sin \omega \, t
\end{eqnarray}\)

コンピューターで軌跡を描いてみると，こんな感じです。

極座標で考えるのですが， \(r = v_0 \, t\) で，また \(\theta = \omega \, t\) です。これから軌跡の式として下記が得られます。

\(\displaystyle
r = \frac{v_0}{\omega} \, \theta
\)

角度と原点からの距離が比例している式です。でもそう言ったからといって軌跡のイメージができるわけではありませんけど。とにかく速度を求めます。

\(\begin{eqnarray} \displaystyle
v_x &=& \frac{d x}{d t} \\
&=& v_0 \, \cos \omega \, t – \omega \, v_0 \, t \, \sin \omega \, t\\
v_y &=& \frac{d y}{d t} \\
&=& v_0 \, \sin \omega \, t + \omega \, v_0 \, t \, \cos \omega \, t\\
\end{eqnarray}\)

よって速度ベクトルは

\(\begin{eqnarray} \displaystyle
\vec{v} &=& \left( v_x , \, v_y \right) \\
&=& v_0 \, \left( \cos \omega \, t , \, \sin \omega \, t \right) + \omega \, v_0 \, t \, \left( – \sin \omega \, t , \, \cos \omega \, t \right)\\
&=& v_0 \, \vec{e_r} + \omega \, v_0 \, t \, \vec{e_{\theta}}
\end{eqnarray}\)

この式は先ほどの極座標で表した速度の式 \(\displaystyle \vec{v} = \frac{d r}{d t} \, \vec{e_{r}} + r \, \frac{d \theta}{d t} \, \vec{e_{\theta}} \) と比較される式ですが，この螺旋の式の場合 \(r = v_0 \, t\) で， \(\theta = \omega \, t\) なので確かに \(\displaystyle \frac{d r}{d t} = v_0\) で \(\displaystyle r \, \frac{d \theta}{d t} = v_0 \, t \, \omega\) となって先の計算の通りです。

　加速度を求めます。

\(\begin{eqnarray} \displaystyle
a_x &=& \frac{d v_x}{d t} \\
&=& – 2 \, \omega \, v_0 \, \sin \omega \, t – {\omega}^2 \, v_0 \, t \, \cos \omega \, t\\
a_y &=& \frac{d v_y}{d t} \\
&=& 2 \, \omega \, v_0 \, \cos \omega \, t – {\omega}^2 \, v_0 \, t \, \sin \omega \, t\\
\end{eqnarray}\)

よって加速度ベクトルは

\(\begin{eqnarray} \displaystyle
\vec{a} &=& \left( a_x , \, a_y \right) \\
&=& 2 \, \omega \, v_0 \, \left( – \sin \omega \, t , \, \cos \omega \, t \right) – {\omega}^2 \, v_0 \, t \, \left( \cos \omega \, t , \, \sin \omega \, t \right)\\
&=& 2 \, \omega \, v_0 \, \vec{e_{\theta}} – {\omega}^2 \, v_0 \, t \, \vec{e_r}
\end{eqnarray}\)

\(r = v_0 \, t\) であることを考えると後ろの項は円運動の向心加速度です。前の項は形から言えばコリオリの力に関する加速度のように見えますが . . . . .

このあたりで，3日目の終わり。

例題 2.1

　(1) は座標を表す式が与えられて，速度や加速度を求めるもの。微分して行く方は分かりやすいと思うので，ここはパスしても良いかなと思う。
　(2) は速度が与えられて，移動距離を求める。積分する方なので取り扱う。速度の式は下記。

\(v(t) = v_0 – a \, t.\)

速度がゼロとなる時刻を \(t_0\) として (\(t_0 = v_0 / a\)），\(t_A \lt t_0 \lt t_B\) となる時刻 \(t_A\) から時刻 \(t_B\) までののべの走行距離を求める。教科書の解答に誤植があるので注意。正誤表にあるのだが，下記が正しい解答です。

\(\displaystyle \frac{a}{2} \, \left\{ \left( t_0 – t_A \right)^2 + \left( t_B – t_0 \right)^2 \right\}\)

e-learning 練習問題02

　教科書とは別に e-learning で練習問題を実施する。下記がその問題。演習としては簡単なものですが，次の3章で運動の法則に入るので，その前にガリレオの話をするのも良いかなと思う。

簡単に，ガリレオの話をする。PDFを用意した。それを使いながらの説明。ガリレオは重力による落下運動を一様な加速運動と考えたが，一様な加速には二つの可能性があると考えた。ひとつは落下距離に比例して速度が増加する場合と，もうひとつは時間に比例して速度が増加する場合である。しかし距離に比例する場合には，どのような距離を落下する場合にも必要となる時間が同じ時間となり観察と矛盾する（距離に比例する速度となる場合は単振り子の運動のような場合です）。それでもうひとつの時間に比例するとして仮説を立て，有名な斜面の実験を試みた。
　斜面上とは言え落下する物体の速度を測ることは難しかったことから，ガリレオは物体が通過する距離とそれにかかる時間の関係を観測します。またこれとは別の方法でも実験していて，それが上の問題にある等しい時間間隔で音を鳴らすようにベルを配置する実験です。\(v – t\) グラフを書いてその面積を使って考えればすぐ分かるのですが，ベルの間隔は奇数の並びとなります。

３章 力と運動

3.1 ニュートンの第１法則（慣性の法則）

　PDFを用意した（PDFの内容はアリストテレスの力学とガリレオの慣性の法則に関する思考実験，同じくガリレオの加速度と力に関する実験の説明）。
　慣性の法則とは，一般的には「物体は力が働かなければ，速度が変化しない」と言った内容です。よく考えたらここまでの話では運動を記述するのみで，力に関して定義も何もしていないのですが，いきなり“力が働かなければ . . .”となります。こうして文章にしてみるとその辺のいい加減さに気づきます。でもそのまま常識的な“力”というイメージが存在するものとして続けます。
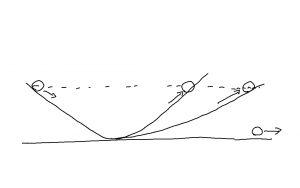
　アリストテレスの力学では力と速度の関係として，力が強ければ速さも大きい。力が止めば運動も止まる，というような理解をしていました。日常的には妥当な感じです。ただそれでは説明できない現象もあって，例えばボールを投げるとき，手を離れたボールが飛び続けるのは何故かといった問いには答えることができませんでした。

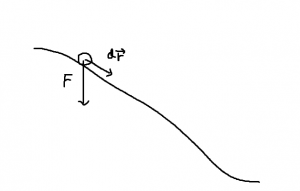
　これに対して，ガリレオは坂道を下ったボールが摩擦で勢いを失うことがなければ，また同じ高さまで坂道をのぼると考えられることから（上図），のぼり坂の傾きをゆるくするとより遠くまでボールが進むことになるので，坂の傾きがなくなった水平の状態では減速せずどこまでもボールが進み続けると結論します。運動は本来持続するものだという主張ですが，ニュートン以前に，すでにこのような理解があったようです。
　慣性の法則を，“力と速度は関係がない”と言い表すと，その歴史的文脈での役割がはっきりするように思えます。力によって運動は生じるものですが，速度や力という概念を明確に定義するレベルに達したとき，力と速度は無関係であると考える段階に入ったということではないでしょうか。それでは，力と関係しているのは何か。それが運動の第２法則で述べられます。
　教科書では，ここに質量に関する記述が入るのですが，これを上手く話の流れに載せることができません。何か良い方法を考えないと。

3.2 ニュートンの第２法則（運動方程式）

　ガリレオは斜面での落下運動を考察しました。斜面の傾きを大きくすると加速度も大きくなります。これは物体を引く力が大きくなるからですが，その力は斜面上に物体を静止させるときに必要となる力で示されます（下図）。

https://catalogue.museogalileo.it/gallery/PlaneWithVariableInclinationInv1402.html

一方で，ガリレオは重い物体も軽いものも落下速度は同じということを知っていました。重さが2倍になると力も2倍になるわけですが，加速度が同じであると言うことは物体の重さ自体に加速度を減少させる働きがあることになります。そんな所から下記の関係が導かれて来たのだと思います。

\(\displaystyle \mathrm{加速度} \propto \frac{\mathrm{力}}{\mathrm{質量}} \)

　地球上の重力に限らず，万有引力のもとでの運動は物体の質量に依存しません。地球も小さな石ころも太陽の引力のもとでは同じ軌道をたどり，同じ幾何学的な軌跡を描きます。

教科書では，このあと運動量に関する記述があります。運動量の話をどこでするのかは考え物です。ニュートンは第２法則を“運動の変化が力に比例”と表現していて(変化率ではない)，それは式で表現すれば

\(\displaystyle m \, \Delta v = \vec{F} \, \Delta t.\)

“力に比例”における“力”も力積を表しているようです。力積を使った話としては面積速度一定の話があります。

このときは力積で考えているといって良いのではないかと思います。このあたりの話で運動量を導入しておけば，作用反作用にうまくつながるかもと考えています。

3.3 ニュートンの第３法則（作用反作用の法則）

　やっとここにたどり着きました。この法則が最も説明が難しいと思います。第１法則では速度と力は関係がない，第２では力と関係するのは加速度だときて，第３の作用反作用の法則はどのような位置づけなのかよく分からない。

　きっかけは衝突の問題だったのかもしれないとも思うのですが，衝突に関してはホイヘンスの研究があって，ニュートン以前から議論されています。

　衝突の際，物体が速度を得るとき，逆にもう一方の物体は速度を失います。速度の変化量はそれぞれの質量に依存するのですが，運動量の変化は同じ大きさで反対向きです（高校で運動量保存を学んでいるし，衝突の問題を解く際には運動量保存の式を立てるので，失う量と得る量が等しいことに学生は納得すると思う）。第２法則と合わせて考えるとそれは２物体に反対向きの力が作用したことを意味します。つまり \(\displaystyle m \, \Delta v = \vec{F} \, \Delta t\) から，運動量の変化が等しければ力積が等しい。衝突にかかる時間も共通しているはずだから，力も等しくなります。
　ただ第１，第２法則からのつながりという点はやはりはっきりしない。

　第１法則と第２法則では“力”という言葉は現れるのですが，それは抽象的に扱われているように思えます。力というものが物体の外部にあって物体と無関係な何か抽象的な作用として扱われているように思えます。力学における力とは万有引力や衝突などで作用する力です。遠隔的であったり近接作用であったりしますが，いずれにせよ他の物体によってもたらされる作用です。そのため力学的世界を完成させるためには，この二つの物体を一緒に取り扱わないといけません。第１，第２法則では一つの物体のみ取り扱いますが，第３法則では初めて二つの物体が登場します。二つの物体がお互いに力を及ぼしあうときのルールを定めてのち，力学的世界が完成するのではないかと思います。これが第３法則の役割かなと考えています。

このあたりで，4日目の終わり。

3.4 いろいろな力

　以下，３章の終わりに向けて，万有引力，摩擦力，弾力（バネの力）が例示される。どれも高校で習う内容なので例題や章末の演習問題をやれば良いかなと思う。ただし既知の内容だけに新奇性やおもしろさを加えることが難しく思える。

万有引力

　円運動の加速度 \(\displaystyle \frac{v^2}{r}\) はホイヘンスが見つけています。運動の第２法則から対応する力 \(\vec{F}\) が分かりますが，これとケプラーの第３法則 \(T^2 \propto r^3\) を組み合わせます。

\(\begin{eqnarray} \displaystyle
\vec{F} &\propto& \frac{v^2}{r} \\
&\propto& \frac{1}{r} \, \left( \frac{2 \, \pi \, r}{T} \right)^2\\
&\propto& \frac{1}{r^2}
\end{eqnarray}\)

太陽と惑星間の引力が軌道半径の逆２乗に比例すると導かれます。

ここで地球と月の関係を考えてみます。月の軌道半径は \(r = 3.85 \times 10^8 \,\mathrm{m}\) ，公転周期は \(T = 27.3 \,\mathrm{日}\) 。よって速度は \(v = 1025 \,\mathrm{m/s}\) 。これから加速度 \(a\) は

\(\begin{eqnarray} \displaystyle
a &=& \frac{v^2}{r} \\
&=& 0.00273 … \,\mathrm{m/s^2}
\end{eqnarray}\)

地球上の重力加速度が \(g = 9.80 \,\mathrm{m/s^2}\) であり，これを地球の引力によるものと解釈します。地球の半径は \(R = 6.37 \times 10^6 \,\mathrm{m}\) で，月の軌道半径のところでこの引力が，太陽と惑星間の力と同じように，距離の二乗に反比例して弱くなるとすると

\(\begin{eqnarray} \displaystyle
g \, \left( \frac{R}{r} \right)^2 &=& 9.80 \times \left( \frac{6.37 \times 10^6}{3.85 \times 10^8} \right)^2\\
&=& 0.00268 … \mathrm{m/s^2}
\end{eqnarray}\)

ほぼ同じ値になったので，地球の重力と太陽ー惑星間の引力が同一の性質を持つものであると結論できます。ただこの計算は授業中にはやらないかも。この後の演習と内容が重なるので概要の話だけで良いかもしれない。どこかできちんとした万有引力の式を見せないといけない。

\(\displaystyle F = – G \, \frac{M \, m}{r^2}\)

例題 3.1

　(1) ケプラーの第３法則を導く問題。万有引力の式が分かっているものとする。円運動の加速度と運動の第２法則から， \(T^2 \propto r^3\) を求める。ほぼ教科書の通りなので計算過程は省略します。この後 pssc 物理の p332 にある表１「ケプラーの第三法則」を学生にみせる。

　(2)と(3)はパス。

重さ

　ここでは，重さと質量の違いを確認するぐらいかなと思う。高校の物理でも習いますので学生もある程度その違いを意識していると思います。この日の課題として，月面と地表での重さの違いを扱うので，その準備の意味もあります。

　重さとは物体が星の中心に向かって引き寄せられる力のことで，地表では \(m \, g\) です。アリストテレスの理論では物体が落ちるのは自然な運動と考えられていて，強制的な力による運動と区別されていました。つまり，その頃重さは力とみなされていなかったということでしょうか。

　月面では加速度が \(1.67 \, \mathrm{m/s^2}\) で \(g\) に相当する部分が小さいので重さも小さくなります。地球の周りを周回する人工衛星や宇宙船の中では重さがゼロになります。そのため体重を秤で測定することができなくなります。下のリンクは国際宇宙ステーションでの体重測定の様子です。

加速度を測っているとテロップがでますので，往復運動をしているようですが周期や振動数を測っているのではないようです。周期だったら \(\displaystyle 2 \, \pi \sqrt{\frac{m}{k}}\) で式に \(g\) が出てこないので，測定する環境に影響されないのですが。

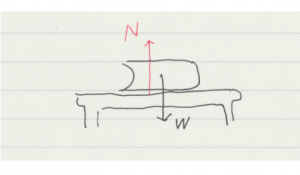
垂直抗力

　これは納得しにくい力です。机の上に本があるとして，本の重さが机を押しているのは分かりますが，机が本を押し返しているのは分かりにくい。本が秤に載せられているときのように，バネで支えられているならまだ分かりやすいのかもしれない。

　もう少しミクロなレベルで観測すれば，本の重さによって机もわずかにへこんでいることが分かります（観測したことないけど）。実際はその弾性の力で机は押し返していると考えて良いようです。ただその変形を考えることにあまり意味がなくて無視して取り扱っています。糸の張力も同じように取り扱います。糸は力が加わることでわずかに伸びているのですが，その変形を考えても運動を考える上では意味がないと言うことで伸びを無視して取り扱います。こういった力は束縛力といわれます。

　演習は次の摩擦力をやってからの方が良いかな。

摩擦力

　解説はしなくても良いのではないかと思う。演習のみでどうだろうか。

演習問題 [7]

　斜面を傾けていって物体がすべり始める角度から摩擦係数をだす問題。最大静止摩擦の係数は滑り始める角度 \(\theta\) の \(\tan \theta\) になる。この問題では，36度の傾きで，静止摩擦係数が \(0.727 …\) となる。

　教科書の表 3.1 にある摩擦係数の値には，テフロン上の鉄の摩擦係数として \(0.04\) があげられている。この場合の斜面の角度は\(2.29\) 度となり，かなり小さい。

弾力

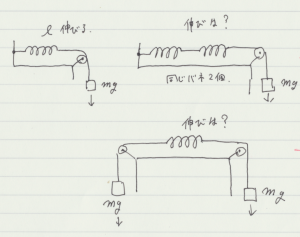
　変形を元に戻す際の力ですが，これはほぼ学生は知っていることと思うので，下記のような問題を考えてもらうぐらいでどうかと思う。

結構間違う。とくに両側におもりをつるした場合に二倍伸びると考える学生が一定数居る。

このあたりが5日目か？

中間試験直前演習

3章演習問題 [5]

　エレベーターの中で鞄を提げているという状況で，上昇下降時の腕に加わる力を求める問題。最初に運動方程式を立てて，後は上昇時，下降時の加速度をあてはめる。

３章演習問題 [7]

　初速 \(20 \, \mathrm{m/s}\) のホッケーパックが \(120 \, \mathrm{m}\) 滑って停止した。このときの摩擦係数を求める問題。 \(v – t\) 図を書いて停止するまでの時間を求め，そこから加速度をだすのがはやいし分かりやすいが，敢えて下記のように加速度から積分をして座標までたどり着く感じで解答しよう。

\(\begin{eqnarray} \displaystyle
a &=& – \mu’ \, g\\
v &=& \int a \, dt\\
&=& \int – \mu’ \, g \, dt\\
&=& – \mu’ \, g \, t + C
\end{eqnarray}\)

２章演習問題 [3]

　やり残していた２章の演習問題に戻る。1次元の運動で座標の時間変化がグラフとして与えられている。(1) はグラフから平均の速度を求める。(2) はグラフから速度を求める問題だがグラフに接線を引く必要があって，やや曖昧な解答になる。(4) の後で解答しても良いと思う。(3) はグラフの式を求める問題。2次式であると限定されているので明確に定まる。(4) は等加速度運動であることを示す問題。微分して速度を出し，速度を微分して加速度を出す。微分を使うところが演習のポイント。

２章演習問題 [4]

　\({v_1}^2 – {v_2}^2 = 2 \, a \, s\) を導く問題。この式は思い出しておいた方が良い。6章のエネルギーの話にも繋がっている。

２章演習問題 [8]

　等速円運動の問題。半径が不明の円形道路を自動車が \(72 \mathrm{km/h}\) で走る。角速度，円の半径，向心加速度を求める。

中間試験

教室で試験をやれなくて，第２大講義室で実施する。

4章 いろいろな運動（１）

4.1 重力のもとでの運動１（放物運動）

　地表での重力による運動に関しての話だが，放物線となることは高校で十分に学習済みだし，何を話すべきか？次の 4.2 では微分方程式を解くということを初めて扱うので，そこは時間をかけるべきと思う。

運動方程式

　地表での物体が受ける力は，その質量に応じて

\(\vec{F} = (0, m \, g)\)

そこから運動方程式は

\(\begin{eqnarray} \displaystyle
m \, \frac{d^2 x}{d t^2} &=& 0\\
m \, \frac{d^2 y}{d t^2} &=& – m \, g\\
\end{eqnarray}\)

これらの式から，(4.5)式や(4.6)式で表される，速度と座標に関する式が得られるが，すでに学習済みということでここでは詳細は話さない。ただ \(x\) 方向と \(y\) 方向を独立に扱って良いことを取り上げる。

ここで，TA 作成の動画を見てもらう。動画は3つの内容が含まれる。ひとつは大きな球も小さな球も同じ速さで落下すること，二つ目は同時に二つの球を自由落下と水平方向に打ち出した場合二つの球が縦方向は同じ運動をしていること，三つ目はモンキーハンティングである。

上の動画は説明しようとしすぎて，良く分からなくなっているような感じです。落下実験なので一瞬で終了して，それで良く分からない映像が続くのですが，良く分からないものを繰り返し見ているとなぜかおもしろく思えてきます。

上記動画で，自由落下と水平方向に同時に打ち出された二つの球が縦方向は同じ運動をしていることを考えてみる。高校の頃はこのことを実験事実として扱っていたのかもしれない（記憶が曖昧）。水平方向に打ち出された球の初速と同じ速度で等速運動する観測者から見ると（細かいことはさておいて）球は自由落下しているように見える。つまり等速運動をしている観測者が見る現象は同じだということを示しています。ガリレイ変換の話なのですが，少しここで対称性という言葉をだしてみたらどうかと思う。放物運動の軌道と例題4.1はパスしても良いかなと思う。

4.2 重力のもとでの運動２（空気抵抗の影響）

　最初に空気抵抗のモデルに関して話してみる。教科書では速度の2乗に比例する慣性抵抗を乱流の効果によるものと記述しているが，講義では流体との衝突による力積として説明した。つまり，速度 \(v\) で流体と衝突して，流体の速度がゼロから \(v\) へ変化する（これは逆に物体を静止させておいて流体を速度 \(v\) で運動していると考える方が分かりやすい。衝突によって流体の速度がゼロになると考える）。この衝突の力積は \(v\) に比例するが，速度は衝突回数にも効いてきて，それはまた \(v\) に比例するので，その積を考えて \(v^2\) に比例すると説明した。速度が比較的小さい場合に現れる粘性抵抗に関しては，簡単な説明をしたのみ。物体の速度が遅く流体が物体表面に沿って層状に流れ，流体中に速度差が生じるような場合の抵抗のモデルである。なぜ速度に比例するのかは私には良く分かっていないが，流体を引きずるイメージなのだろうか？速度差から摩擦のような力が想定できるが，そうすると速度に依存する摩擦力ということになる。

　このあと，速度に比例する方の粘性抵抗の場合を解いてみる。雨滴が落下する場合の運動方程式（微分方程式）を変数分離を使って解いてみる。

\(\displaystyle m \, \frac{d v}{d t} = m \, g – c \, v\)

計算において\(c\) を \(m \, k\) で置き換えているが，最終的には \(k\) を使用していないので意図が良く分からない。計算は教科書のものの隙間を埋めるぐらいで，まあそのまま。下記の雨滴の速度の式のグラフを説明して終了。

\(\displaystyle v = \frac{m \, g}{c} \, \left( 1 – \exp \left( – \frac{c \, t}{m} \right) \right)\)

以前は変数分離の説明を先にやっていたが，学ぶことが多くなりすぎる気がして今回は止めた。

4.3 束縛力の働く運動（束縛運動）

　束縛力に関しては以前少し話しているが，多少内容を繰り返した。垂直抗力や張力などが束縛力と言われるが，名前の由来として，運動方向を限定する力であることと，実際は多少机がたわんだり糸が伸びて多少変形し，その復元力なのであるが，その変形を取り扱うことにあまり意味が無いので，その変形を無視して力のみを取り扱うと説明した。

斜面上の滑空運動と垂直抗力はパスして，単振り子と張力へ進む。

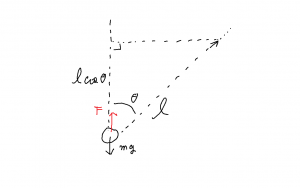
単振り子と張力

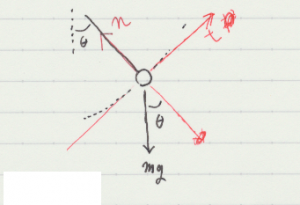
　ここは，教科書をなぞるように解説するのみ。束縛力の例であり，その例にふさわしく座標軸を都合の良い方向にとる。振り子の振れ角を \(\theta\) として，その糸の伸びる方向（ｎ）と振り子の軌道の方向（ｔ）の２方向で運動方程式を組み立てる。

軌道半径を \(l\) として，方程式は下記の式となる。

\(\begin{eqnarray} \displaystyle
m \, a_t &=& m \, l \, \frac{d^2 \theta}{d t^2} = – m \, g \sin \theta\\
m \, a_n &=& m \, l \, \left(\frac{d \theta}{d t} \right)^2 = T – m \, g \cos \theta
\end{eqnarray}\)

振り子の運動とともにｎ方向とｔ方向が変化してしまうのがいやな気がする。藤原邦男先生の『物理学序論としての力学』の87ページをみると極座標で記述している。その方程式は下記。

\(\begin{eqnarray} \displaystyle
m \, a_r &=& m \, \left( \frac{d^2 r}{d t^2} – r \, \left( \frac{d \varphi}{d t} \right)^2 \right) = m \, g \cos \varphi – T\\
m \, a_{\varphi} &=& m \, \frac{1}{r} \, \frac{d}{d t} \, \left( r^2 \frac{d \varphi}{d t} \right) = – m \, g \sin \varphi
\end{eqnarray}\)

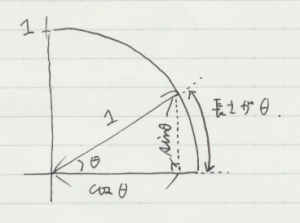
\(r = l\) で \(r\) が一定であるので，教科書の式と同じものになる。つまり途中の過程を省略しているということなのだろう。教科書では36ページで円運動の場合の極座標での加速度を計算している。

\( \displaystyle
\vec{a}= – r \left(\frac{d \theta}{d t} \right)^2 \, \vec{e_{r}} + r \, \frac{d^2 \theta}{d t^2} \, \vec{e_{\theta}}
\)

このそれぞれの基本ベクトルの係数に，\(a_t\) や \(a_n\) が現れている。この結果を引用するところから話を始めてみる手もある。しかしその場合はいきなり極座標での加速度を取り扱うことになって学生は戸惑うかもしれない。教科書に沿って計算した後で，36ページの結果を振り返る方が良いかもしれない。

次に振り子の運動方程式を解くのだが，そこで使用する \(\sin \theta \approx \theta\) の解説をした。

この近似を用いるとｔ方向の方程式が下記となる。

\( \displaystyle
\frac{d^2 \theta}{d t^2}= – \frac{g}{l} \, \theta\\
\)

これを解くわけですが，教科書では詳しい話をせず一般解を与えている。講義では，線型性や高校で学習した三角関数の知識と絡めた話にしてみたらどうかと考えて，以下の様に話した。

　二回微分して元の形が現れるので，当てはまるものといえば三角関数で，例えば下記。

\( \displaystyle
\theta = A \, \cos \alpha t
\)

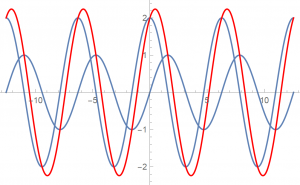
\(A\) は任意定数で，また \(\displaystyle \alpha = \sqrt{\frac{g}{l}}\) であれば良いのですが， \(\theta = B \, \sin \alpha t\) もまた解で，さらにその和 \(\theta = A \, \cos \alpha t + B \, \sin \alpha t\) も解です。三角関数の和がどんなものかグラフを書いてみます。

上記は \(2 \, \cos \theta + \sin \theta\) のグラフで，赤い線が和のグラフです。グラフを見ると三角関数の和はやはり同じ周期の三角関数になっていて，ただしピークの位置が異なります（位相がずれています）。これらは高校の数学で学んだ，下記の三角関数の合成式に相当する話です。

\( \displaystyle
a \, \sin \theta + b \, \cos \theta = \sqrt{a^2 + b^2} \, \sin \left(\theta + \alpha \right)
\)

同じ文字を使って分かりづらいのですが，ここで \(\displaystyle \alpha = \tan^{-1} \frac{b}{a}\) です。結局一般解は

\( \displaystyle
\theta = A \, \cos \left( \sqrt{\frac{g}{l}} t + \delta \right)
\)

任意定数が2つ含まれるので一般解だという話は数学の授業に委ねました。後は下記の周期の式を見せて，

\( \displaystyle
T = 2 \, \pi \sqrt{\frac{l}{g}}
\)

周期に質量も振幅も現れないことを話して終わりました。

4.4 往復運動（単振動）

　高校で単振動について学んでいるし，先の振り子の話と計算が重なることもあって話しづらい。しかし物理に詳しくない学生もいることを考慮して，とりあえず何の話か最初に明確にして始める必要はある。

ばねの弾力による単振動

ばねの絵を書いて座標 \(x\) の取り方や力の向きの話をして復元力の式をみせる。

\( \displaystyle
F = – k \, x
\)

　上記から運動方程式が下記のようになる。

\( \displaystyle
m \, \frac{d^2 x}{d t^2}= – k \, x
\)

これを解いて，下記。

\( \displaystyle
x = A \, \cos \left( \omega \, t + \alpha \right)
\)

ここで \(\displaystyle \omega = \sqrt{ \frac{k}{m} }\) です。周期は下記。

\( \displaystyle
T = 2 \, \pi \sqrt{\frac{m}{k}}
\)

今度は周期に質量が現れて，でも振幅は現れない。何か高校の頃学んだこととは違った話を織りこんだ方が良いかと考えて，なぜ振幅が変わっても周期が変化しないのかという話をやってみた。

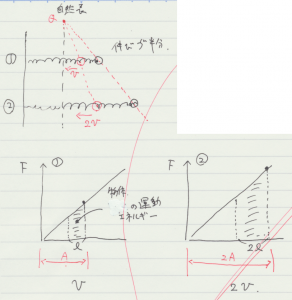
上の図の様に，振幅を二倍にした場合に，運動の様子がどのように変化するのかを考える。ばねが自然長に戻るときの速さを比較すると，エネルギー保存則から振幅の大きい方が二倍の速さになることが分かります。これはばねの縮み具合がどの長さの場合にも当てはまります。例えば振幅が小さい方が変位最大のところから \(l\) 縮んで，振幅の大きい方が \(2 \, l\) 縮んだときの速さをそれぞれ求めてみます。ばねの力学的なエネルギーは \(F – x\) のグラフの面積で表されるので，ばねが縮んだときの運動エネルギーはエネルギー保存則から，変位が最大の三角形の面積から底辺が \(l\) 短くなった三角形の面積を引いた残りの台形の面積に相当します。これを振幅の大きい方にも当てはめて考えると，台形の面積は振幅の小さい方の台形の四倍になっていて，つまり速さは二倍にであることが分かります。これから，振幅の大きい方の運動は振幅の小さい方の運動を二倍に拡大したようなものだということが分かります。高校で単振動を学ぶとき等速円運動の射影であると教わりますが，その射影するスクリーンまでの距離を二倍にしたような運動です。

　上記のような説明をしたのですが，学生の反応は悪かった。\(F – x\) のグラフの面積がエネルギーであることは，多くの学生が高校で学習済みであるとして話したのですが，そのあたりはどうだったのか不明です。それよりは，自然長に戻ったときに大きい振幅の方が速さが二倍であるということから，これはどの変位の位置でも言えることだと説明抜きで示唆するだけにして，高校のときの単振動の説明と同じように等速円運動の射影を持ち出して，スクリーンまでの距離が二倍になった運動に相当すると話す方が良いのかもしれない。こちらの方が周期が変わらないことが納得しやすいように思われる。

4章 演習問題 [6]

　宿題との関連で，演習問題の[6]をやる。エネルギー保存則は6章で学ぶのだが，この問題ではエネルギー保存則を使わざるを得ない。

　問題は，最下点での速さを \(v_0\) として，振り子の振れ角 \(\phi\) と張力 \(T\) の関係を求めるもの。張力が現れる式としては69ページ(4.42)式があって， \(\theta\) を \(\phi\) に入れ替えて

\(\displaystyle
m \, a_n = m \, l \, \left(\frac{d \phi}{d t} \right)^2 = T – m \, g \cos \phi .
\)

上記の \(\displaystyle \frac{d \phi}{d t} \) は角速度なので，速度と関連している。ある振れ角 \(\phi\) での速さはエネルギー保存則で求められて，

\(\displaystyle
v^2 = {v_0}^2 – 2 \, g \, l \, \left( 1 – \cos \phi \right) .
\)

これを利用して，振れ角と張力の関係式が求められる。課題は下記のような問題でした。

課題は易しすぎるかもしれませんが，基本的な事項の確認ができれば良いかなと考えています。

4章 演習問題 [5]

　スカイダイバーの落下運動の問題。速度の2乗に比例する慣性抵抗である。変数分離を用いる例としてやった方が良いと思う。運動方程式は下記となる。

\(\displaystyle
m \frac{d v}{d t} = m \, g- b \, v^2 .
\)

先に，時刻無限大での終端速度を導いておく。速度が大きくなるにつれて，加速度が小さくなり，だんだんと下記の速度に近づいていく。

\(\displaystyle
v_{\infty} = \sqrt{\frac{m \, g}{b}}.
\)

後は，変数分離で解くのみ。

\(\displaystyle
\frac{d v}{1-\frac{b}{m \, g} \, v^2 } = g \, d t.
\)

\(\alpha = \sqrt{\frac{b}{m \, g}}\) として，左辺の分母を積の形にする。

\(\begin{eqnarray} \displaystyle
\frac{1}{\left(1-\alpha \, v \right) \left(1+\alpha \, v \right)} \, d v &=& g \, d t\\
\frac{1}{2} \, \left\{ \frac{1}{1-\alpha \, v } + \frac{1}{1+\alpha \, v } \right\} \, d v &=& g \, d t
\end{eqnarray}\)

後は積分して下記を得る。

\(\displaystyle
\frac{1}{2} \, \left\{-\frac{1}{\alpha} \, \log \left| 1-\alpha \, v \right| + \frac{1}{\alpha} \, \log \left| 1 + \alpha \, v \right| \right\} = g \, t + C
\)

上記を式変形し時刻ゼロで速度がゼロという条件を考慮して，下記の速度の式が得られる。

\(\displaystyle
v = v_{\infty} \, \frac{1-\exp \left(\frac{- 2 \, g \, t}{ v_{\infty}} \right)}{1+\exp \left(\frac{- 2 \, g \, t}{ v_{\infty}} \right)}
\)

4章 演習問題 [9]

3つのばねで床と天井の間に等しい間隔で支えられている物体がある。この振動の周期を求める問題。

まず，最初にこのばねは伸びているのか縮んでいるのか気になります。これに関しては，重力を加えた力の釣り合いを考えたとき，自然長より縮んでいることはあり得ないと見て取れます。

　長さ \(l\) の状態のばねの力を \(F_0\) として，物体を上方に \(\Delta x\) 動かすとします。ばねは \(\Delta x\) 縮むとき力が \(k \, \Delta x\) 減少し，伸びるとき \(k \, \Delta x\) 増加します。

もともと重力を含めた合力は釣り合っていたので，上向きを力の正方向として下記が成り立っていました。

\(\begin{eqnarray} \displaystyle
\mathrm{合力} &=& F_0 + F_0-F_0- m \, g\\
&=& 0
\end{eqnarray}\)

物体を上方に \(\Delta x\) 動かすとき，合力はゼロではなくなり下記のように下向きの力となります。

\(\begin{eqnarray} \displaystyle
\mathrm{合力} &=& F_0-k \, \Delta x + F_0-k \, \Delta x-\left(F_0 + k \, \Delta x \right) – m \, g\\
&=& – 3 \, k \, \Delta x.
\end{eqnarray}\)

負の力ですから，物体の移動方向とは反対向きの力が生じています。この力をひとつのばねの復元力だと見なせば振動の周期が分かります。

６章 エネルギーとその保存則

　エネルギーと仕事の章。最初にエネルギーや仕事というものを見つける話をしたいと思うが，そう考えるとイントロに悩む。多くのテキストが仕事の定義から入っている。物理では仕事というものをこのように定義する ….等の記述の後，式計算から仕事と運動エネルギーの関係を導いている。これ以外の入り方はないものか。
　章のどこかで，仕事とはエネルギーの移動であることを述べるようにする。

運動の法則から，力によって運動が変化するということを学びました。

\(\displaystyle
m \, \frac{d v}{d t} = F.
\)

上の式は瞬間の話です。力が継続したらどうなるのかというと p45 の(3.8)式のように運動方程式を時間で積分することで，

\(\begin{eqnarray} \displaystyle
\int_{t_1}^{t_2} m \, \frac{d v}{d t} dt &=& \int_{t_1}^{t_2} F dt\\
m \, v_2- m \, v_1 &=& \int_{t_1}^{t_2} F dt.
\end{eqnarray}\)

上記は，力積と運動量変化の関係です。これは運動方程式が直接意味するところと，そう変わりません。それでは時間で積分する以外には考えられないものでしょうか。そもそも運動方程式はなぜ微分方程式なのでしょうか。微分する前の形というものがあるのでしょうか。結論を言うと，それは座標による積分と関係しています。

\(\displaystyle
\int F d x
\)

先ほどは時間で今度は座標です。これは仕事といわれる量です。運動方程式の左辺の積分は運動エネルギーとなりますが，その計算はこの章の(6.5)でやります。

6.1 仕事

　以下，中学，高校で既に仕事という概念を学習済みであるということが前提になっている説明。もっと根本からの話をやりたいところ。

　以下，仕事の例をあげて，その定義の復習をやっていきます。

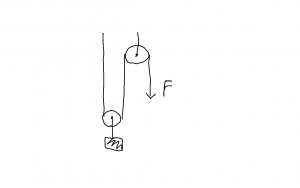
　力と作用した距離の積は，滑車の話で出てきます。上図のように滑車を組み合わせると，持ち上げる力は半分になりますがひもを引く距離は倍になります。それでは楽になったとは言えない。『マッハ力学』（p45）では，このことを，機械を使って仕事を節約することはできないと表現していて，力と距離の積が重要であることが，このような現象から理解されて来たのだと思います。講義では，積が重要なのだから，積の値が同じであることに意味がある（何らかの等価性を示している）という点を協調すべきと思う。

　もう一つの例をあげます。初期の蒸気エンジンの性能を示すのに，時間あたりどれぐらいの水を汲み上げるのかという指標がありました。1 分間で 3300 ポンドを1 フィート持ち上げるとかです（1 馬力）。時間あたりなので仕事率に相当するものですが，1 分間という枠をはずせば，物理の中での仕事の概念とぴったりです。

　この章ではエネルギーという概念も出てくるのですが，エネルギーという言葉は，蒸気エンジンが登場して後の言葉です。もちろん \(m \, v^2\) が運動を表す上で重要であることは，デカルトやライプニッツの頃から意識されていました。ただあてはまる名称が無かったということは，動力を作り出すエンジンが登場するまで，その意識は力学の中にとどまっていたということかと思います。

　教科書の解説は，何かの力に逆らって物体を移動させるという話ではないのですが，以下では重力に逆らって水を汲み上げるということを例として，仕事について考えてみましょう。図のように（水を単純な丸い物体として書きました），重力に逆らって持ち上げるなら，必要な力は重力と同じ大きさで反対向きとなります。それで十分です。後は定速でゆっくりと移動すると考えます。つまり力が釣り合っている状態で持ち上げます。

移動する方向は重要です。力が釣り合っているので自由にどの方向にも移動できます。しかし水平に移動しても水を汲み上げたことにはなりません。重力と逆の方向に移動した距離が重要です。図に示すように \(l\) 移動したとしても重力と逆方向に移動した距離 \(l \, \cos \theta\) が有効な仕事（持ち上げた高さ）です。これが距離に \(\cos \theta\) をかける理由です。この仕事は \(F \, l \, \cos \theta\) となります。

　釣り合いの状態意外で移動させることも考えられますが，その時は物体に運動エネルギーの増加ももたらします。

先ほどの仕事 \(F \, l \, \cos \theta\) は，ベクトルの内積を使って表せます。移動を \(\vec{l}\) として，仕事は

\(\begin{eqnarray} \displaystyle
\mathrm{仕事} &=& F \, l \, \cos \theta\\
　　　　　　&=& \vec{F} \cdot \vec{l}
\end{eqnarray}\)

仕事の定義の復習はここで終わり。

変化する力による仕事－ばねを引き伸ばすための仕事

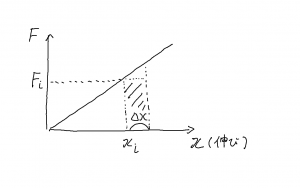
一定の力ではなく強さが変化する場合の仕事の求め方。ばねを例として取り上げる。結果を学生は知っているだけに興味を持たせることが難しく思える。

力－変位のグラフを示し，微小変位 \(\Delta x\) 伸ばした場合の仕事 \(\Delta W_i\)

\(\displaystyle
\Delta W_i = F_i \, \Delta x
\)

上記は下のグラフの短冊の面積に相当する。

そのため，自然長から \(x\) までばねを伸ばすときに \(F\) がする仕事 \(W\) は

\(\begin{eqnarray} \displaystyle
W &=& \sum_{i} F_i \, \Delta x\\
W &=& \sum_{i} k \, x_i \, \Delta x
\end{eqnarray}\)

\(\Delta x\) を小さくすることで，上記の和を積分に置き換える。

\(\begin{eqnarray} \displaystyle
W &=& \int_{0}^{x} k \, x’ \, dx’\\
W &=& \frac{1}{2} k \, x^2
\end{eqnarray}\)

結局，力－変位のグラフの面積を求めたことを協調した。それは学生はすでに知っていることかもしれないが，次の「6.2 仕事の一般的定義」で仕事の計算に線積分を使うので，積分との関連を強調した方が良いと思う。それだけが目的かも。

6.2 仕事の一般的定義

　仕事の計算を直線上だけでなく，それ以外の自由な曲線上の経路で考える。移動経路を微小な部分に分割して，それぞれの微小変位での仕事を計算しその和を求める。なぜ仕事がスカラーとして足し算可能なものであるのかという理由は説明しない。仕事とエネルギーの関連はまだ出てきていないので，足し算をどのように学生はイメージするのだろうか。先のばねを伸ばすときの仕事の計算でも微小仕事の和を考えた。直線上ではあまり気にならなかったが，曲線上で和を考えるとき，仕事がスカラーでありその和にも意味があることを，暗黙のうちに仮定していることが気になる。これを解消する始め方というのがあるのか。

　教科書では一般的な話として，任意の曲線に沿って移動する場合の仕事の定義を与えている。とりあえず最初は教科書の入りを読んで計算方法の大まかなところをみた後，具体的に万有引力のもとでの移動の話として説明してみた。そこに違いはないのかもしれないが，具体的な話の方が取り扱わなければならない必然性はあるように学生は感じるのではないか。

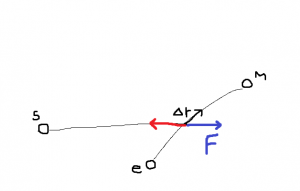
太陽（S）の引力に逆らって地球（e）から火星（M）まで移動する。上図の \(\Delta r\) 移動するときの仕事は，引力（赤）と反対向きで同じ大きさの力を \(\vec{F}\) として

\(\displaystyle
\Delta W_i = \vec{F}(\vec{r}_i) \cdot \Delta \vec{r}_i
\)

全体の仕事 \(W\) は

\(\begin{eqnarray} \displaystyle
W &=& \sum_i \Delta W_i\\
&=& \sum_i \vec{F}(\vec{r}_i) \cdot \Delta \vec{r}_i
\end{eqnarray}\)

\(\Delta r_i\) を小さくして

\(\displaystyle
W = \int_{\mathrm{地球}}^{\mathrm{火星}} \vec{F}(\vec{r}) \cdot d \vec{r}
\)

学生はまだ線積分を習っていないので，積分を成分ごとの計算に分ける。

\(\displaystyle
W = \int F_x \, d x + \int F_y \, d y + \int F_z \, d z
\)

上記なら計算できる。この分けた積分の計算が次の「重力がする仕事」につながる。

重力がする仕事

　ここは教科書の記述とほぼ同ように話す。スキーヤーが雪の斜面を高さ \(h\) 滑り降りるときに重力がする仕事を求める話。先の記述にあった仕事を求める線積分を具体的に計算する例。今まで，重力に逆らって移動させる仕事を考えてきたが，ここでは重力がする仕事を求めるので話が反対になっている。学生は戸惑わなかったのだろうか。

力と変位のベクトルの記法は教科書から少し変える。

\(\displaystyle
\vec{F}(\vec{r}) = ( 0, – m \, g), \quad d \vec{r} = (d x, d y)
\)

全体の仕事は

\(\begin{eqnarray} \displaystyle
W &=& \int \vec{F}(\vec{r}) \cdot d \vec{r}\\
&=& \int F_x \, d x + \int F_y \, d y\\
&=& \int_{h}^{0} – m \, g \, dy\\
&=& m \, g \, h
\end{eqnarray}\)

斜面の形が計算には全く出てこなかったことから，経路に依らない値であることを強調した。この後の保存力の話への伏線のつもり。

仕事率

　ここは簡単に，ワットの話でもすれば良いのではないかと思う。ただし，力学における仕事率は力と速度の積なのだが，教科書は仕事を時間で割った計算を示しているだけで，瞬間の計算をきちんとすればその記述は間違いではないのだが，幾分注意が必要かもしれない。そういえば，仕事の単位（ジュール）の話を全然していなかった。

　単位時間あたりの仕事について考える。講義ではこれから出てくる話だが，仕事はエネルギーに変わり，それゆえ単位時間あたりの仕事は単位時間あたりのエネルギーの送出や消費の話につながる。

\(\Delta t\) の間に \(\Delta W\) の仕事をするとして，仕事率 \(P_{AV}\) は

\(\displaystyle
P_{AV} = \frac{\Delta W}{\Delta t}
\)

力学では， \(\Delta t\) で \(\Delta \ell\) 移動する場合，速度を \(v\) として

\(\begin{eqnarray} \displaystyle
\Delta W &=& F \, \Delta \ell\\
&=& F \, v \, \Delta t.
\end{eqnarray}\)

　
それゆえ，仕事率 \(P\) は

\(\begin{eqnarray} \displaystyle
P &=& \frac{\Delta W}{\Delta t}\\
&=& \frac{F \, v \, \Delta t}{\Delta t}\\
&=& F \, v.
\end{eqnarray}\)

　これからすると一定の力を加え続ける等加速度運動でも，速度の増加と共に仕事率は増加している。最終的な運動エネルギーを加速に要した時間で割っても仕事率は得られない。

　上の計算で力が作用した距離を考える際に速度と微小時間の積を考えたが，これはこの後の運動方程式の積分を考えるときに似たようなことをやるので，その前振りになるかも。

6.4 保存力と位置エネルギー

　例題 6.1 を先に挟むかどうか悩むところだけど，今回は挟まない。ここは具体的な例から入りたい。保存力となる具体的な例から入りたい。それにしても，なぜ保存力をここで持ち出してくるのか，いつものことながらその理由付けが難しい。理由付けは要らないのだろうか。本を読んでいるときは確かにあまり理由付けは要らないような気がするが，いざ講義で話し始めると，なぜこの話をするのかという理由が欠けていると非常にやりにくい。

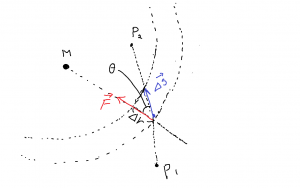
　先に，重力がする仕事は高さの差のみで決まり経路に依らないというのがあった。逆に重力に逆らって持ち上げるときも，斜面との摩擦が無視できるのであれば必要な仕事は経路に依らない。万有引力もまた同様である。下図のように，星 M からの引力により P1 から P2 まで移動するときに，万有引力がする仕事を考える。

移動する経路のうち，ふたつの同心円を横切る区間 \(\Delta \vec{s}\) での仕事 \(\Delta W\) は

\(\begin{eqnarray} \displaystyle
\Delta W &=& \vec{F} \cdot \Delta \vec{s}\\
&=& \left|\vec{F}\right| \cdot \left|\Delta \vec{s}\right| \, \cos \theta\\
&=& \left|\vec{F}\right| \, \Delta r.
\end{eqnarray}\)

このふたつの同心円をどのように横切ろうと仕事は変わらない。加えて同心円の円周に沿って移動するときは \(\theta = 90^{\circ}\) なので仕事はゼロである。それゆえどの経路を通ろうと万有引力のする仕事は同じ値になる。また逆に引力に逆らって移動する場合も同様に必要な仕事は経路に依らない。このように仕事が経路に依らない力を保存力という。

　保存力という名前はいかにも何か保存される量と関わりがあるのだろうという感じがしますが，仕事を求めた計算の積分範囲の始点（以下では \(\vec{r_0}\) ）を固定すれば，座標だけで決定されるスカラー関数 \(U \left( \vec{r} \right)\) が考えられます。

\(\begin{eqnarray} \displaystyle
W \left( \vec{r}, \vec{r}_0 \right) &=& – \int_{\vec{r}_0}^{\vec{r}} \vec{F} \cdot d \vec{r}\\
U \left( \vec{r} \right) &=& – \int_{\vec{r}_0}^{\vec{r}} \vec{F} \cdot d \vec{r}.
\end{eqnarray}\)

　 \(U \left( \vec{r} \right)\) は位置エネルギーやポテンシャルエネルギーなどと言われる量です。またこの保存力のもとで，任意の2点間を移動するときに必要な仕事を \(U \left( \vec{r} \right)\) を用いて表してみます。

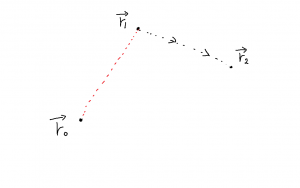
どの経路で仕事を計算しても同じ値になるのだから， \(\vec{r}_0\) から出発して \(\vec{r}_1\) を経由し \(\vec{r}_2\) に至る経路で仕事を計算します。

\(\begin{eqnarray} \displaystyle
W \left( \vec{r}_2, \vec{r}_1 \right) &=& – \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d \vec{r}\\
W \left( \vec{r}_2, \vec{r}_0 \right) – W \left( \vec{r}_1, \vec{r}_0 \right)&=& – \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d \vec{r}\\
U \left( \vec{r}_2 \right) – U \left( \vec{r}_1 \right)&=& – \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d \vec{r}
\end{eqnarray}\)

この式はこの後のエネルギー保存のところで使います。

6.5 運動方程式のエネルギー積分

　6 章の始めから仕事に関して考えてきて，ここでやっと運動と仕事が結びつきます。運動方程式は

\(\displaystyle
m \frac{d \vec{v}}{d t} = \vec{F}
\)

上記のように微分の式なのですが，微分する前の形が存在するのか。また仕事は運動方程式の右辺を座標で積分した形をしています。

\(\displaystyle
\int \vec{F} \cdot d \vec{r}
\)

左辺を座標で積分するとどうなるのか，というのがここの内容です。

1次元の運動

　最初は 1 次元で考えましょう。力は座標で決まるものを想定します。一次元なので運動方程式は下記。

\(\displaystyle
m \frac{d v}{d t} = F(x).
\)

仕事は右辺を座標で積分したものなので，両辺を座標で積分してみます。

\(\displaystyle
\int m \frac{d v}{d t} \, d x = \int F(x) \, d x.
\)

右辺は仕事そのものなのでほっといて，左辺を計算してみます。まずは積分の変数変換。

\(\begin{eqnarray} \displaystyle
d x &=& \frac{d x}{d t} \, d t\\
&=& v \, d t
\end{eqnarray}\)

これを用いて左辺を計算すると

\(\begin{eqnarray} \displaystyle
\mathrm{左辺} &=& \int m \, \frac{d v}{d t} \, v \, d t\\
&=& \frac{m}{2} \, \int_{t_1}^{t_2} \frac{d}{d t} \left( v^2 \right) \, d t\\
&=& \frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2}
\end{eqnarray}\)

\(v_1\) ， \(v_2\) は時刻 \(t_1\) ， \(t_2\) での速度です。右辺と合わせると下記。

\(\displaystyle
\frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2} = \int_{x_1}^{x_2} F(x) \, d x.
\)

（ 仕事が正の値ならば）仕事を加えることで \(\displaystyle \frac{1}{2} \, m \, v^{2}\) が増加しています。これが仕事と運動の関係です。やっと落ちが付きました。

　 \(F(x)\) が保存力であるとして，下記のようにポテンシャルエネルギーを定義します。

\(\displaystyle
U \left( x \right) = – \int_{x_0}^{x} F(x’) \, d x’.
\)

先ほどの右辺の仕事を，この \(U(x)\) を用いて表すと

\(\begin{eqnarray} \displaystyle
\int_{x_1}^{x_2} F(x) \, d x &=& \int_{x_0}^{x_2} F(x) \, d x-\int_{x_0}^{x_1} F(x) \, d x\\
&=& – U(x_{2}) + U(x_{1}).
\end{eqnarray}\)

上記で右辺を置き換えると，結局

\(\begin{eqnarray} \displaystyle
\frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2} &=& – U(x_{2}) + U(x_{1})\\
\frac{1}{2} \, m \, v_{2}^{2} + U(x_{2}) &=& \frac{1}{2} \, m \, v_{1}^{2} + U(x_{1})
\end{eqnarray}\)

保存力による運動では，\(\displaystyle \frac{1}{2} \, m \, v^{2} + U(x)\) が一定の値となっています。それでこの一定の値として保持されている何かにエネルギーという名が付きました。

運動エネルギー

　ここは先ほどの仕事と運動の関係を 3 次元にしただけです。

下記の運動方程式の両辺を上図の経路に沿って座標で積分することを考えます。

\(\displaystyle
m \frac{d \vec{v}}{d t} = \vec{F}
\)

右辺の積分は仕事そのものです。

\(\displaystyle
\int \vec{F} \cdot d \vec{r}
\)

ここで \(d \vec{r} = (d x, d y, d z)\) です。続いて左辺の積分を考えてみましょう。

\(\begin{eqnarray} \displaystyle
\mathrm{左辺} &=& \int m \, \frac{d \vec{v}}{d t} \cdot d \vec{r}\\
&=& \int m \, \frac{d v_x}{d t} \, d x + \int m \, \frac{d v_y}{d t} \, d y + \int m \, \frac{d v_z}{d t} \, d z
\end{eqnarray}\)

ここで項のひとつだけを取り出してみます。

\(\begin{eqnarray} \displaystyle
\int m \, \frac{d v_x}{d t} \, d x &=& \int m \, \frac{d v_x}{d t} \, v_x \, d t\\
&=& \frac{m}{2} \, \int_{t_1}^{t_2} \frac{d}{d t} \left( v_{x}^2 \right) \, d t\\
&=& \frac{1}{2} \, m \, v_{x}^{2}(t_2)- \frac{1}{2} \, m \, v_{x}^{2}(t_1)
\end{eqnarray}\)

よって左辺は

\(\displaystyle
\mathrm{左辺} = \frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2}
\)

右辺と繋ぎます。 \(\vec{F}\) が保存力であるとして，そのポテンシャルエネルギーを \(U\) とすれば，

\(\begin{eqnarray} \displaystyle
\frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2} &=& \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d \vec{r}\\
\frac{1}{2} \, m \, v_{2}^{2}- \frac{1}{2} \, m \, v_{1}^{2} &=& – U \left( \vec{r}_2\right) + U \left( \vec{r}_1\right)\\
\frac{1}{2} \, m \, v_{2}^{2} + U \left( \vec{r}_2\right) &=& \frac{1}{2} \, m \, v_{1}^{2} + U \left( \vec{r}_1\right)
\end{eqnarray}\)

1 次元と同じようにエネルギー保存則が成立しました。

例題 6.1

　さて，仕事の計算です。慣れない線積分をやってみるという例題ですが，結局成分に分けて計算してしまうので通常の積分とあまり変わりがありません。

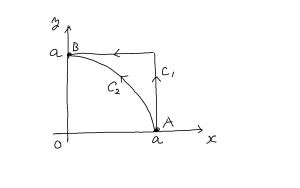
　質量 \(m\) の物体が，力 \(\vec{F} = (-k\, y, k \, x)\) を受けて，下図のような平面上を点 A から点 B まで移動します。変数 \(k\) を付けているのは次元（単位）を考えてのことだと思います。

C1の経路（正方形の辺上）とC2（円周上）で仕事を計算します。力がどんな感じのものなのか少し考えてみます。位置ベクトルと力の式から，両者が直交していることが分かります。

円周上では（半径 \(r\) ），力は大きさが一定で，接線方向に向いています。 \(r\) が大きくなるにつれて，力も大きくなります。

\(\begin{eqnarray} \displaystyle
\vec{F} &=& \sqrt{k^2 \, x^2 + k^2 \, y^2}\\
&=& k \, r
\end{eqnarray}\)

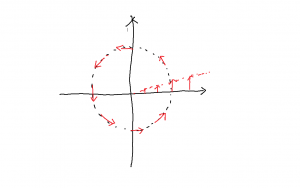
そのため，力は下図の様に渦を巻いています。原点から遠ざかるほど力は大きくなります。

まずは C1 に沿って，仕事を計算してみましょう。C1 上で \(\displaystyle \int \vec{F} \cdot d \vec{r}\) を求めます。 \(d \vec{r} = (d x, d y)\) として，\(\vec{F}\) との内積を考えます。

\(\begin{eqnarray} \displaystyle
\int_{C_1} \vec{F} \cdot d \vec{r} &=& \int_{C_1} F_x \, d x + \int_{C_1} F_y \, d y\\
&=& \int_{a}^{0} – k \, a \, d x + \int_{0}^{a} k \, a \, d y\\
&=& – k \, a \, \Bigl[\, x \, \Bigr]_{a}^{0} + k \, a \, \Bigl[\, y \, \Bigr]_{0}^{a}\\
&=& 2 \, k \, a^2
\end{eqnarray}\)

次に C2 上で計算してみましょう。変数変換をしたいのですが， \(\vec{r} = ( x, y) = (a \, \cos \theta, a \, \sin \theta)\) として，

\(\begin{eqnarray} \displaystyle
d \vec{r} &=& ( d x, d y)\\
&=& ( -a \, \sin \theta \, d \theta, a \, \cos \theta \, d \theta)
\end{eqnarray}\)

また力は

\(\begin{eqnarray} \displaystyle
\vec{F} &=& ( – k \, y, k \, x)\\
&=& ( -k \, a \, \sin \theta, k \, a \, \cos \theta)
\end{eqnarray}\)

よって

\(\begin{eqnarray} \displaystyle
\vec{F} \cdot d \vec{r} &=& k \, a^2 \, \sin^2 \theta \, d \theta + k \, a^2 \, \cos^2 \theta \, d \theta\\
&=& k \, a^2 \, d \theta
\end{eqnarray}\)

上記を使って仕事を計算します。

\(\begin{eqnarray} \displaystyle
\int_{C_2} \vec{F} \cdot d \vec{r} &=& \int_{0}^{\frac{\pi}{2}} k \, a^2 \, d \theta\\
&=& k \, a^2 \, \Bigl[ \, \theta \, \Bigr]_{0}^{\frac{\pi}{2}}\\
&=& \frac{\pi}{2} \, k \, a^2
\end{eqnarray}\)

C3 もあったのですがパスします。さて，上記二通りの計算から，経路によって仕事の値が異なる結果となりました。それゆえこの力は保存力ではありません。保存力は位置エネルギーと関連した力です。位置エネルギーの勾配として，坂を下る方向に力が定義されます。それゆえ力に相当する勾配を与える等高線が考えられないと保存力ではありません。この例題の力は渦を巻いていました。渦巻き状の力を与える等高線を引くことは不可能ですね。

例題 6.3

　計算が大変ですが，これをやります。いつものことながら計算だけで講義中に時間がかなりかかりそう。計算を講義中にやることは意味があるのかとよく考えますが，計算しないと説得力が無いような気がして，やはりやることになります。どう考えるべきか。

　問題は，力学的エネルギー保存則の式を変形して，次の関係式を導け，というものです。

1. 重力のもとで鉛直方向に運動する物体の高さ \(z(t)\)
   　　　　　　\(\displaystyle z(t) = z_0 \pm v_{0} \, t-\frac{1}{2} \, g \, t^2\)
2. 長さ \(\ell\) の糸におもりを付けた単振り子の運動方程式
   　　　　　　\(\displaystyle \frac{d^2 \theta}{d t^2} = – \frac{g}{\ell} \, \sin \theta\)

1. は下記の式から始めて

\(\displaystyle
\frac{1}{2} \, m \, \left( \frac{d z}{d t} \right)^2 + m \, g \, z = \frac{1}{2} \, m \, v_{0}^2 + m \, g \, z_0
\)

\(z(t) = . . .\) の形に変形していきます。途中で変数分離を使います。計算は教科書のままなので此処に書きません。

2. は下記の式から始めて

\(\displaystyle
\frac{1}{2} \, m \, \left( \ell \, \frac{d \theta}{d t} \right)^2 + m \, g \, \ell \, \left( 1-\cos \theta \right) = \mathrm{一定}
\)

上記の両辺を時間で微分します。これも計算がほぼ教科書のままなので此処に書きません。

　ただ授業ではエネルギー保存則を時間で微分したら運動方程式になったことを強調したい。例題の解答とは別に 1. のエネルギー保存則の式を時間で微分することをやってみます。再掲ですが

\(\displaystyle
\frac{1}{2} \, m \, \left( \frac{d z}{d t} \right)^2 + m \, g \, z = \frac{1}{2} \, m \, v_{0}^2 + m \, g \, z_0
\)

上記の両辺を時間で微分します。

\(\begin{eqnarray} \displaystyle
m \, \left( \frac{d z}{d t} \right) \, \frac{d^2 z}{d t^2} + m \, g \, \frac{d z}{d t} &=& 0\\
m \, \frac{d^2 z}{d t^2} &=& – m \, g
\end{eqnarray}\)

こちらも微分することで運動方程式が得られました。6 章の最初で話した，運動方程式の元となる式としてエネルギー保存則の式が挙げられるということで落ちを付けたい。

　だいたいこのあたりで講義は終了かと思います。後は演習と期末試験だけ。最後の日に（不吉な）再試の話を忘れない。再試用の演習問題を期末試験終了後に Moodle にアップすることを連絡する。