誤差論ノート
実験の最初は誤差の話ですが,ここでは誤差の見積もりについて
私自身の直感的なイメージを書いてみます。以下,内容の目次です。
内容
- 測定値の広がり
- 直感的に,誤差をどのようにとらえるか
- 測定値から真の偏差は求めることができない
- 平均値の広がり
- 誤差の見積り
- 誤差の伝播
- 資料:β線の計測結果
(1)測定値の広がり
実験で,繰り返し測定をすると,ある範囲に散らばった値が得られます。測定回数が多くなれば,誤差論でそのまま取り扱えるような理想的なデータとなりますが,そんな場合はまれです。図1は,そのまれの場合で,Srから放射されるβ線をGMカウンターで計測したものです。10
秒間の測定を1万回繰り返して,平均して950個程度の値が得られています。これぐらい測定をすれば,実験の全容がわかります。この分布の形は正規(ガウス)分布といわれるもので,誤差の話の主役です。
図1
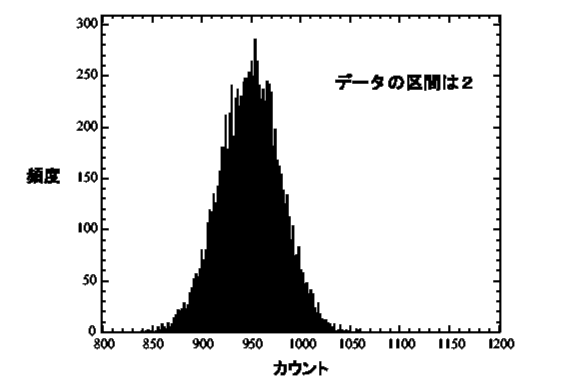
注:β線の計測は,本来確率的な現象ですから、正規分布ではなくポアソン分布と考えるのが適当で,それ故測
定値に真の値は存在しないし,誤差についても考えにくいのですが,以下では真の値が存在し正規分布をなしているとします。
正規分布は、中心の値と広がりの幅の二つで決まります。中心の値は実験では,真の値(aで表します)と言われます。ここではすべての計測の平均値(948.2)を真の値としますが、本当は無限回の測定の平均値のことです。測定値の広がりは分布の高さが,ピークの値の\(\displaystyle \frac{1}{\sqrt{e}}\)倍(eはオイラー数)になるところで定義されています。この幅は偏差σと言って以下のように計算します。また,偏差を2乗したものを分散といいます
\( \displaystyle \sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i – a)^2}{n}} \)
ここでxiは測定値,nは測定回数ですが,ここでは測定回数を無限大と考えています。図2に示すように、このσの幅を考えると,どのような分布でも正規分布であれば,測定値の約7割がこの範囲に入ります。図1のβ線の実験の偏差は30.8です。7割入っているでしょうか?
図2
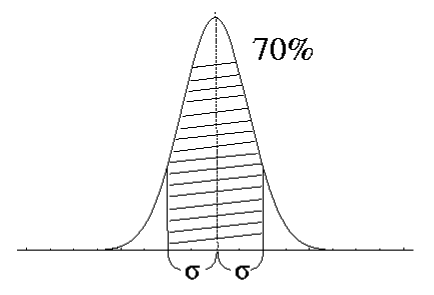
測定すると言うことは,正規分布をしている無限個のサンプルの中から,どれかを抜き出すことです。例えば,このページの最後の方に1000回分の測定結果を付けますが,この中から数値を抜き出すことに相当します。9回の測定であれば9個の数値をランダムに抜き出すことに対応します。以下,9個抜き出しました。
さて,この平均値の誤差はどのぐらいでしょうか?そもそも誤差とは何でしょうか?ものの本によると,誤差の定義は,測定値と真の値との差,となっていて,ようするに測定値とピークの値との差です。この平均値も測定値のひとつですから,図2によれば,ピークの位置から左右にσの幅を考えるとき,7割の確率でこの範囲の中にあります。これを逆に平均値を固定して考えると,平均値から左右にσの幅をとれば,その幅の中に7割の確率でピークがあると言い換えて良いでしょう(図3)。つまり平均値が分布の山の右端付近にある場合と左端付近にある場合を両極端と見なしているわけです。
結局,誤差とは偏差だと言うことですね。
図3
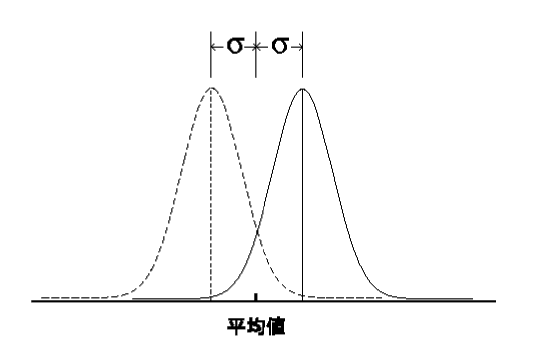
誤差を決めるのはσだと予想したのは良いのですが,σを求めるには無限回の測定をしなければいけません。9回の測定では”真の偏差”からほど遠いですが,これは矛盾です。無限回測定すれば真の値そのものも得られますから。誤差など考える必要がありません。
9回の測定値から何とかしなければいけませんが,ここで”平均値からの偏差”とでも呼ぶべき値を計算してみましょう(本当はちゃんと名前があると思います)。真の値との差ではなく,平均値との差を元にして下記の計算をしてみます。
\(\displaystyle \sqrt{\frac{\sum_{i=1}^{n} (x_i – \bar{x})^2}{n}}\)
この値は40.6となって,“真の偏差”30.8と同じぐらいです。これを偏差の代わりとして用いても良さそうです。そこでこの計算を見直して,二つの偏差の関係を考えてみます。めんどくさいので,測定回数を3回にへらします。最初は真の偏差を計算する式から始めて,平均値からの偏差の形を無理矢理つくります。
\( \displaystyle \sigma^2 = \frac{(x_1 – a)^2 +(x_2 – a)^2 +(x_3 – a)^2}{3} \)
上式を,平均値を用いて書きかえ,また \(\bar{x} – a = b\) として
\(\begin{eqnarray*}
\sigma^2 &=& \frac{1}{3} \left\{ (x_1 – \bar{x} + \bar{x}- a)^2 + \cdots \right\} \\
&=& \frac{1}{3} \left\{ (x_1 – \bar{x})^2 + 2 (x_1 – \bar{x}) b + b^2 + \cdots \right\} \\
&=& \frac{1}{3} \left\{ (x_1 – \bar{x})^2 + \cdots \right\}+ \frac{2 b}{3} \left\{ x_1 – \bar{x} + \cdots \right\} + b^2 \\
&=& \frac{1}{3} \left\{ (x_1 – \bar{x})^2 + \cdots \right\} + b^2\\
\mathrm{分散} &=& \mathrm{平均値からの分散} + b^2 \mathrm{ ….. 式1 }
\end{eqnarray*}\)
先の計算によると、偏差と“平均値からの偏差”は同じぐらいの大きさでした。これを式1と考えあわせると、b の大きさはσと比較して小さいことが
分かります(それどころか虚数になっていますが,この辺は誤差の範囲)。 つまり平均値と真の値との隔たりはσに比較して小さく、図3の見積もりは幅が広すぎるようです。
これは,平均値には平均値の分布があることを意味しています。平均値の広がりはσの幅ではありません。
(4)平均値の広がり
平均値の広がりがひとつひとつの測定よりも小さくなるのはありそうなことです。ひとつひとつのバラツキがならされてしまいますから。それじゃ,平均値の偏差は元の偏差とくらべてどれぐらいになるのか?この話は結構難しい。この実験が1年生対象であることを考えると,どのように話したものかと毎年悩みの種でした。2回測定の場合,平均値の偏差がいくらになるのか,これを計算するには2重積分が必要です。実験の教科書では積分を使わずにやっているものもありますが,統計の本で”独立した二つの事象の確率”等のページを見てみると,重積分が使用されています。2回の測定値がそれぞれ独立していますから(無関係だから)x-y平面上のある領域で何かの関数f(x,y)を積分するような計算がでてきます。この計算を講義中にやることは無謀です。何しろ学生は重積分を習ったばかりですから(あるいはまだやっていないかも)。しかし重積分を使用しないと,説明が曖昧なものになってしまいます。実験の教科書のように式の変形だけで話を進めた場合に学生が結論に納得してくれるのか,自信がありません。ここが誤差の話をするときの難しさだと感じていました。
しかし,二つの測定結果を組み合わせてグラフにして,それを眺めているうちに幾何学的な説明が可能だと思い至りました。計算も大学受験程度の数学で良さそうです。
図4
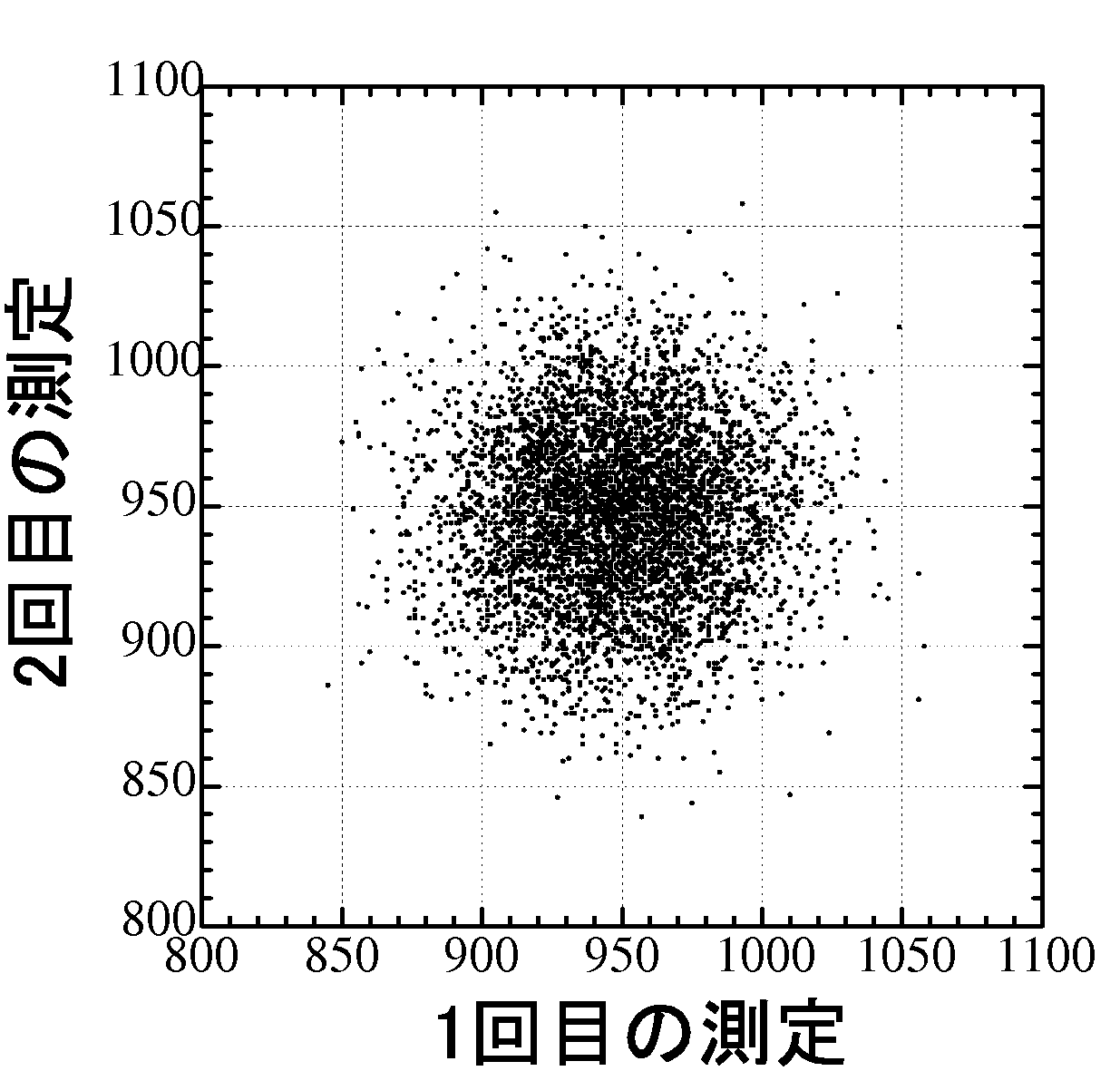
ロットすると図4のようなグラフになります。見たところだいたい円になるわけですが,この円の半径はσかその2,3倍程度の半径になりそうです。つまり、σが範囲の目安ですね。測定値の組はだいたいのところ,半径σの円の中に入ることになりますが,ここで
点(x,y)が円の中の領域にある時,P=x+y,と定義されるPの値の範囲はいくらか
という,問題を思い出して決着しました。円の中心を座標の原点として図を書きかえたものが図5です。
図5
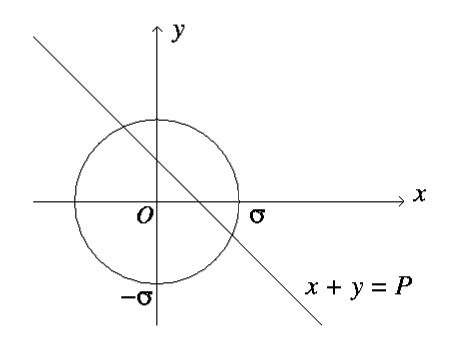
\( – \sqrt{2} \sigma \leq P \leq \sqrt{2} \sigma\)
平均値の分布の範囲は,
\(\displaystyle – \frac {\sigma}{\sqrt{2}} \leq \frac{x+y}{2} \leq \frac{\sigma}{\sqrt{2}}\)
これからすると,2回測定の平均値の偏差は \(\sigma / \sqrt{2}\) になるようです。
(5)誤差の見積もり
n回測定の場合は幾何学的に \(\sigma / \sqrt{n}\) と予想されますが(本当か?)誤差とは偏差のことですから,平均値の誤差b の大きさとして \(\sigma / \sqrt{n}\) の程度が期待されます。これを先の式1に代入してみると(但し、今回はn 回測定として),
\(\begin{eqnarray*}
\mathrm{分散} &=& \mathrm{平均値からの分散} + b^2\\
{\sigma}^2 &=& \frac{\sum {\left(x_i – \bar{x} \right)}^2}{n} + \frac{{\sigma}^2}{n}\\
\left( 1 – \frac{1}{n} \right){\sigma}^2 &=& \frac{\sum {\left(x_i – \bar{x} \right)}^2}{n}\\
{\sigma}^2 &=& \frac{\sum {\left(x_i – \bar{x} \right)}^2}{n-1}
\end{eqnarray*}\)
不思議なことにσが計算できてしまいます。これを再び \(\sigma / \sqrt{n}\) に戻してみると,
\(\displaystyle \frac{\sigma}{\sqrt{n}} = \sqrt{\frac{\sum {\left(x_i – \bar{x}\right)}^2}{n(n-1)}}\)
平均値の偏差,すなわち誤差がでてきました。結局”真の値”は測定の平均値を中心として誤差の大きさを,加えた場合と差し引いた場合の下記の値
\(\displaystyle \bar{x} \pm \sqrt{\frac{\sum {\left(x_i – \bar{x}\right)}^2}{n(n-1)}}\)
この値で区切られる範囲に,約70%の確率で存在することになります。
ここで終わりなら,この方法もただの思いつきにしかすぎないのですが,意外にも間接測定の誤差を考えるときに,ほとんど同じ方法が使えることが分かりました。
(6)誤差の伝播
間接測定とは,その値が直接測れず,測定値から計算して求める場合をいいます。こんな場合に測定の誤差が計算結果にどのように影響するのか考えてみます(このようなことを誤差伝播といいます)。
実験テーマのひとつに”ボルダの振り子”というものがあって,重力加速度を求める実験ですが,その式は下記のようなものです。
\( \displaystyle g = \frac{4 {\pi}^2}{T^2}\left\{l+r+\frac{2}{5}\frac{r^2}{l+r}\right\}\left(1+\frac{{\theta_0}^2}{8}\right)\)
ここで、T は振り子の周期、l は振り子の長さ、r は
金属球の半径、θは振り子の振れ角です。このような値を測って,計算から重力加速度を求めます。間接測定とはこんな感じです。
これを,まともに考えるのは後回しにして,最初は簡単なところから始めましょう。まずは下記のような足し算の式を考えてみます。
\( Z = 2 A + 3 B\)
AとBを測定して,Zを計算する,とします。A,B,Zそれぞれの真の値を添え字ゼロを付けてあらわすと,その間には下記のような式が成立します(まあ,当然といいますか)。
\( Z_0 = 2 A_0 + 3 B_0\)
AとBの誤差をΔA,ΔBとすると,Zの誤差ΔZは下記のように考えます(ΔZの定義)。
\(\begin{eqnarray*}
Z_0 + \Delta Z &=& 2 (A_0 + \Delta A) + 3 (B_0 + \Delta B)\\
\Delta Z &=& 2 \Delta A + 3 \Delta B
\end{eqnarray*}\)
こうしてみると,もともとの計算式にあった係数2,3が誤差の関係式に残って,その係数の大きさに応じてZの誤差に寄与することになっています。この式を眺めてみて,
AとBの偏差がそれぞれσA,σBであれば,ΔAとΔBはこの範囲内で変動して,その場合のΔZの変化の範囲は,
とくれば,もう結論が見えてきます。グラフを書いてみましょう。2ΔAをx座標,3ΔBをy座標として測定点の誤差をプロットします。この場合測定点の組は図6の楕円の中にあるでしょう。
図6
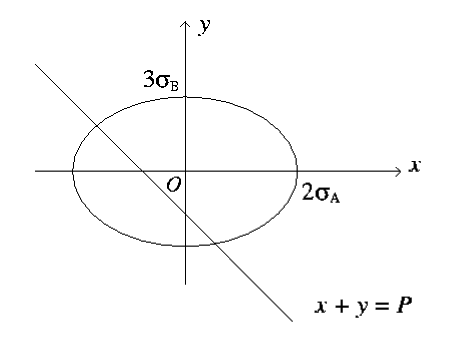
後は,点(x,y)がこの楕円の中にあるとき,P=x+yで与えられるPの範囲を求めれば良いわけです。さすがに今度は幾何学的にとはいかないので,下記の連立方程式を考えます。
\(\left\{
\begin{array}{l}
x + y = P\\
{\left( \frac{x}{2 {\sigma}_A} \right)}^2 + {\left( \frac{y}{3 {\sigma}_B} \right)}^2 = 1
\end{array}
\right.\)
この連立方程式の判別式はこんな感じで,
\(\mathrm{判別式} = -P^2 + 4 {\sigma_A}^2 + 9 {\sigma_B}^2 \)
そうすると,Pの範囲すなわちΔZの範囲は,
\( – \sqrt{(2 {\sigma}_A)^2 + (3 {\sigma}_B)^2} \leq \Delta Z \leq \sqrt{(2 {\sigma}_A)^2 + (3 {\sigma}_B)^2}\)
これでひとまず決着しましたが,この例は非常に簡単な式でした。一般的な話にするために,Z=f(A,B)のような形をしている場合を考えてみます。この場合にはΔZは全微分の要領で,下記のようになりますが,
\(\displaystyle \Delta Z = \frac{\partial f}{\partial A} \Delta A + \frac{\partial f}{\partial B} \Delta B\)
この式を見ると,もはや考えることは何も残っていなかったようです。すでに考え尽くしていました。この一般的な式の場合も,それぞれの測定値の誤差が,微分係数に応じて全体の誤差に寄与してくるでしょうから,Zの偏差は下記のようになるでしょう。
\( \displaystyle {\sigma}_Z = \sqrt{{\left( \frac {\partial f}{\partial A} \right)}^2 {{\sigma}_A}^2 + {\left(\frac{\partial f}{\partial B}\right)}^2 {{\sigma}_B}^2}\)
これですべてが解決です。最初の問題に戻ってみると,結局重力加速度の偏差を求める場合は,下記のような式になりそうですね。
\(\displaystyle \sigma_g = \sqrt{\left(\frac{\partial g}{\partial T}\right)^2 {\sigma_T}^2 +\left(\frac{\partial g}{\partial l}\right)^2 {\sigma_l}^2 +\left(\frac{\partial g}{\partial r}\right)^2 {\sigma_r}^2 + \left(\frac{\partial
g}{\partial {\theta}_0 }\right)^2{\sigma_{\theta_0}}^2}\)
4次元の楕円体でしょうか?
(7)資料:β線の計測結果
β線の1000回分の測定結果を下記にリンクします。
おしまいです。