注意:この実験では、各自測定結果をエクセルを利用して処理します。パソコンを持参するようにしてください。USBメモリを利用して、測定結果を各自のパソコンに移動させます。実験室に用意している USB メモリ端子の形状は Type-A です。Type-c のみのパソコンでは読み取ることができません。その場合はコネクターの形状を変換するものが必要となります。
1. 目的
水上に浮かぶ二つの磁石間の相互作用から、作用反作用の法則に関して理解を深める。
2. 原理
作用反作用の法則は、ニュートンの運動の法則の3番目のものである。中公文庫『世界の名著 26 ニュートン』(プリンキピア)には以下のように記されている。
- 作用に対し反作用は常に逆向きで相等しいこと。あるいは、二物体の相互の作用は常に相等しく逆向きであること
歴史的には先に、物体の衝突の際には運動量が保存されるとの認識があった。それは現在の用語を用いれば、衝突の際にそれぞれの物体がもう一方の物体に与える力積は、大きさが等しく向きが反対であると言いかえられる、これを力の概念を使って言い表せば作用反作用の法則となる。ただしニュートンは衝突のような近接作用だけではなく、万有引力のような遠隔作用にも対象を広げて普遍的法則であるとした。
運動量保存則と作用反作用の法則の関連を見てみる。A、B 二つの物体からなる孤立した系を考える。下記は2次元における 2 物体の重心の座標を表す式である。
- \(\displaystyle x_{\mathrm{G}} = \frac{m_{\mathrm{A}} \, x_{\mathrm{A}} + m_{\mathrm{B}} \, x_{\mathrm{B}}}{m_{\mathrm{A}} + m_{\mathrm{B}}} , \quad y_{\mathrm{G}} = \frac{m_{\mathrm{A}} \, y_{\mathrm{A}} + m_{\mathrm{B}} \, y_{\mathrm{B}}}{m_{\mathrm{A}} + m_{\mathrm{B}}}\)
上記を時間で微分すると
- \(\displaystyle \frac{d \, x_{\mathrm{G}}}{d \, t} = \frac{m_{\mathrm{A}} \, \frac{d \, x_{\mathrm{A}}}{d \, t} + m_{\mathrm{B}} \, \frac{d \, x_{\mathrm{B}}}{d \, t}}{m_{\mathrm{A}} + m_{\mathrm{B}}} , \quad \frac{d \, y_{\mathrm{G}}}{d \, t} = \frac{m_{\mathrm{A}} \, \frac{d \, y_{\mathrm{A}}}{d \, t} + m_{\mathrm{B}} \, \frac{d \, y_{\mathrm{B}}}{d \, t}}{m_{\mathrm{A}} + m_{\mathrm{B}}}\) .
運動量保存則から、上記両式の右辺の分子の項は衝突の際も不変であるから、\(\frac{d \, x_{\mathrm{G}}}{d \, t} , \, \frac{d \, y_{\mathrm{G}}}{d \, t}\) の値は一定値となる。つまり孤立した系では重心は等速直線運動をするか、あるいは最初に静止しているのであれば静止し続ける。また重心の速度が定数であることを考慮して、上式にある運動量の和の式を再び時間で微分すれば、下記の式が得られる。
- \(\displaystyle 0 = m_{\mathrm{A}} \, \frac{d^2 \, x_{\mathrm{A}}}{d \, t^2} + m_{\mathrm{B}} \, \frac{d^2 \, x_{\mathrm{B}}}{d \, t^2} , \quad 0 = m_{\mathrm{A}} \, \frac{d^2 \, y_{\mathrm{A}}}{d \, t^2} + m_{\mathrm{B}} \, \frac{d^2 \, y_{\mathrm{B}}}{d \, t^2} \)
上式に現れる各項はそれぞれ力の成分を表す。A に働く力を \(Fa\) 、B に働く力を\(Fb\) として、上式の各項を置き換える。
- \(\displaystyle 0 = Fa_x + Fb_x, \quad 0 = Fa_y + Fb_y\)
ベクトルとして表せば下記の作用反作用の法則の式が得られる。
- \(\displaystyle \overrightarrow{Fa} = \, – \overrightarrow{Fb}\)
プリンキピアには、磁石と鉄を水に浮かせて実験した例があげられている。それは多少違った文脈であるが、このテーマではニュートンが実施した実験に倣って、水面に浮かべた磁石間の作用反作用を確認してみる。
3. 装置
まず磁石とそれを水面上に浮かべる船として、下図のようなものを使用する。
船にはシャーレを用いる。上図のシャーレ中央の黒い球体が磁石である。シャーレには、位置を検出するために丸い色つきのシールを 3 カ所貼ってある。これらのシールは正三角形の頂点に位置していて、この3点の平均として磁石の位置を定める。磁石は船に固定されておらず、受け皿に置かれているだけである。磁石には南北の極がある。南北が水面と水平になるように磁石を船に配置すれば磁石間の相互作用は大きくなる。
上図のような水槽に水を貯めて、シャーレを浮かべる。水は20リットル程度使用する。磁石の動きは周りの鉄等の磁性体の影響を受ける。机や床には鉄が入っているので、ある程度水深がある方が磁性体との距離が取れる。他には地磁気も考慮する必要がある。磁石の南北の極を地磁気の方向と平行に設置すれば、地磁気による磁石の回転を小さくできる。シャーレの進行方向も地磁気と並行にする方が運動が比較的単純なものとなるので、水槽の長辺を地磁気と並行になるように配置する。
水はポリタンクにあるものを使用する。水を水槽に注入するときやポリタンクに回収する時には、お風呂ポンプを利用する。水を張ったら、磁石を浮かべて地磁気の方向を確認しそれと水槽の長辺が並行になるように調整する。実際に磁石を運動をさせて、回転運動があまり生じないできるだけ単純な運動となる設置方向を探ること。
撮影には USB カメラ(logicool C922n)を用いる。このカメラはズームが可能であるが、この実験では利用しない(最初からズーム状態であれば、デスクトップ上にある logicoolのアプリを利用して解除する)。これを三脚で水槽の真上に固定して、上空から磁石の動きを観測する。カメラから水面までは 70 cm 程度離す。撮影には Windows 付属のカメラアプリを利用する。
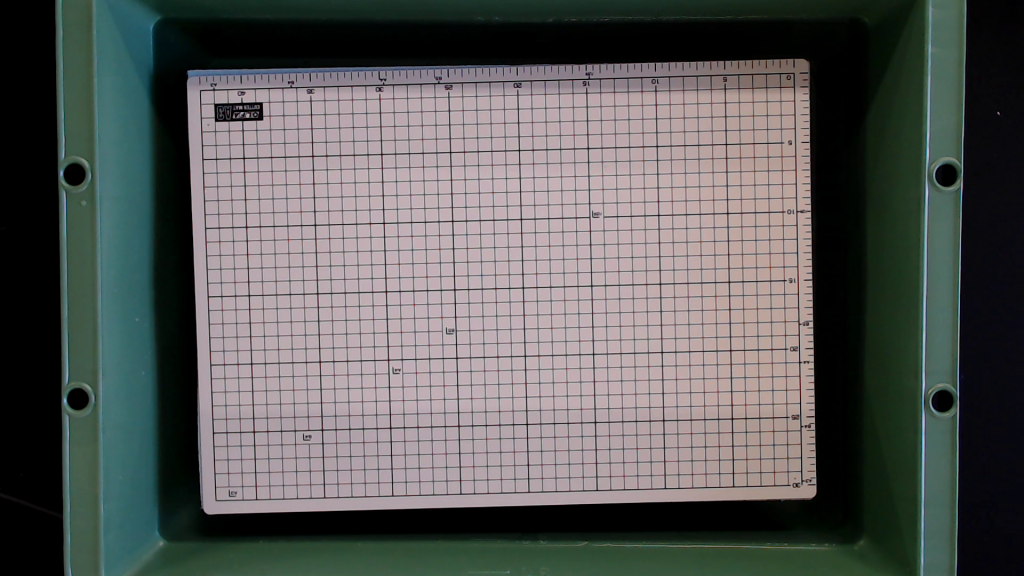
カメラの画像から得られるピクセル座標の値を実際の座標に換算する必要がある。これには下図にある方眼が印刷されているカッティングボードを利用する。
4. 実験と解析
注:実験終了時に提出してもらうものは、報告用のパワーポイントファイルのみです。エクセルファイル等の提出は必要ありません。Moodle に提出先を用意しています。
4.1 衝突動画の撮影
磁石を載せたシャーレを水に浮かべて自由に運動させ、それらが衝突する映像を撮影する。磁石はその極(NとSの向き)を確認して、極を貫く軸がシャーレの面と並行になるようにシャーレ上に置く。そのような配置であれば、磁石間の引力がもっとも強くなる。これらを水面に浮かべて、地磁気の向きを確認し、それと水槽の長辺が平行になるように、水槽の位置と方向を調整する。このようにして、磁石を載せたシャーレがお互いに引き合うとき、水槽の長辺と並行に運動するようにする。
これ以降カッティングマットの撮影終了まで、三脚やカメラの位置を動かさないように注意する。
撮影中にフォーカスが変化してしまうことがあるので、カメラは固定のフォーカスが望ましい。撮影した動画を、下記にひとつあげる。手を用いて磁石を静かにスタートさせるのは難しいが、動画では銅製の針金で適当なものを作り利用している。動画は、各自それぞれが自分の動画を作成する。
下図に銅製の針金の写真をあげる。
先の動画では、このような針金を水中に沈めて利用している。動画としては、下記に示す余分なところを切り詰めた動画を使用した。
4.2 ピクセル座標を実座標に変換する
注意:先の磁石間の引力を撮影した際の USB カメラの位置と同じ位置で下記の撮影を実施することが重要である。動かしてしまうと、引力の撮影からやり直すことになる。また加えていうと、この作業は撮影のみを実施して座標の読み取り等は、次の「4.3 磁石の座標を得る」での待ち時間に実施した方が良いだろう。
下記に重回帰分析を実施したエクセルファイルをあげるので、参考にしてください。
以下、座標軸を定める作業を記述するが、座標軸は測定グループ毎にひとつ定め、グループ内では共通のもので良い。
カッティングボードをスタイロフォームの上にのせて、水面に浮かべる。
この状態を USB カメラで撮影する。撮影は静止画撮影ではなく動画として撮影する。つまり実際に磁石の運動を撮影するときと同じ条件で撮影する。撮影中にフォーカスが外れないように、オートフォーカスではなく固定フォーカスにする。
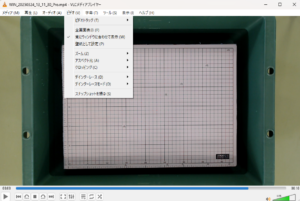
その動画から一枚静止画を切り出して、その瞬間で座標軸を定める。画像の切り出しには VLC プレイヤーを用いる(下図)。VLC プレイヤーで動画を読み込んで適当なところで一時停止をし、ビデオメニューから「スナップショットを撮る」を選んで静止画像を作成する。
座標の読み取りには windows 付属の ペイントを利用する。先のスナップショット画像をペイントで読み込んで、画像上の適当なところにマウスを置くと、下図のようにウインドウの左下にマウスの座標が表示される。
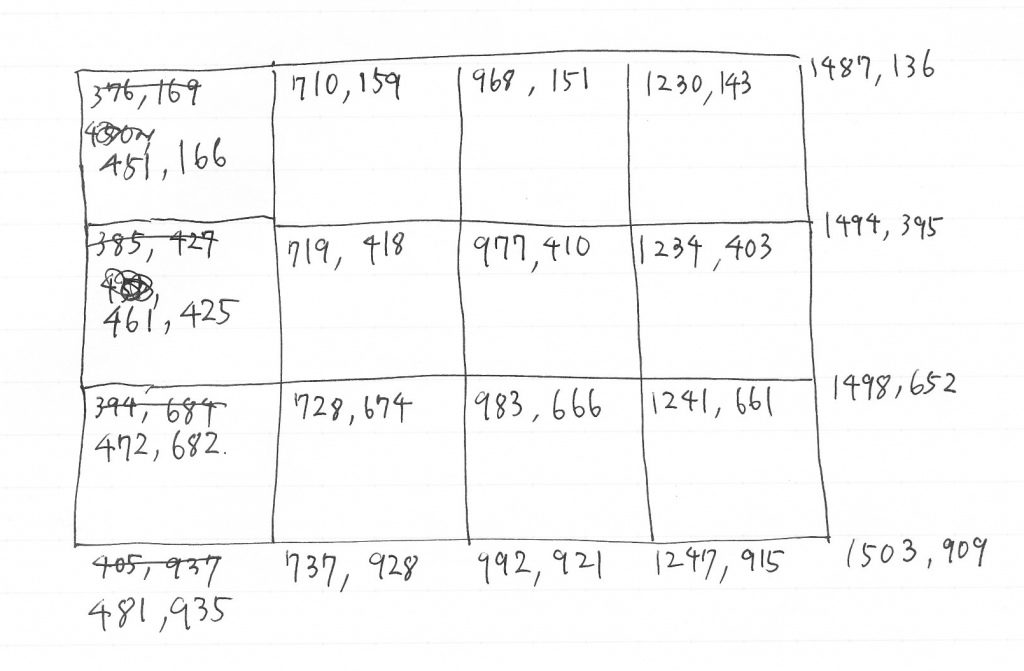
下図のように、10 cm 格子のところのピクセル座標値を読み取る。
上図のピクセル座標 (Px, Py) を、縦が 15 cm ~-15 cm まで 、横が -20 cm ~20 cm までの実座標 (x, y) とする。実座標とピクセル座標の関係式として以下のような式を想定している。
-
x = A + B*Px + C*Py + D*Px^2 + E*Py^2
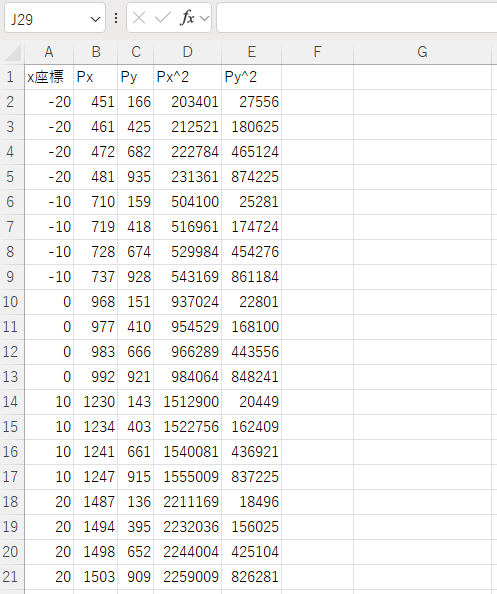
y 座標に関しても同様である。上記の式の係数 A, B, C, D, E を求めるために、Excel で重回帰分析をする。下図は、x 座標をピクセル座標値から決める際のキャプチャーである。2次まで考慮するためにピクセル座標値の2乗の列を追加している。
回帰分析は Excel の「データ」「分析」「データ分析」にある。なければインストールする。
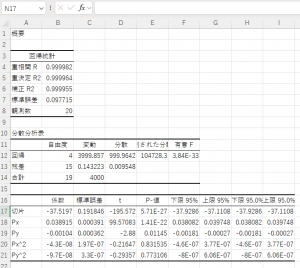
下図が分析結果である。各項の係数が得られた。
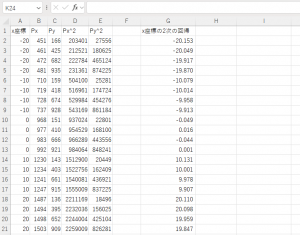
得られた式から、再現した x 座標を計算して比較した結果を下図に示す。右端の列が x 座標の再現値である。
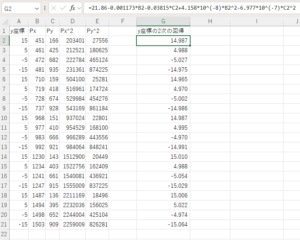
y 座標を得る式も、同様に求める(下図)。
ピクセル座標の測定値と回帰分析によって得られた x, y 座標の式を報告用のパワーポイントファイルに記入する。
4.3 磁石の座標を得る
磁石の座標を読み取るために deeplabcut を利用する。このソフトは元々動物の動きなどを追いかけるためのものである。
(以下の画面キャプチャーは他の動画を解析した際のものである)
windows の start から Anaconda Prompt を起動する。
下図のような端末の画面が開く。
以下のコマンドを端末で打ち、環境を DEEPLABCUT に切り替える。
- conda activate DEEPLABCUT
deeplabcut を起動する。
- python -m deeplabcut
下図が起動画面である。起動には多少時間が必要である。
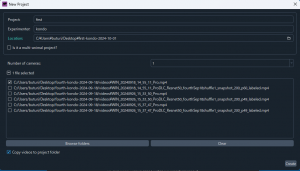
プロジェクトを新しく始めるので、create new project を選ぶ。
プロジェクトに名前を付け、Experimenter に実験する人の名前を記入する。
プロジェクト名、実験者の名前ともに日本語を利用しないようにしてください。エラーが生じます。
これらの情報からファイルを収めるフォルダー名が決まる。デフォルトではデスクトップにフォルダーが作られる。下方では機械学習のトレーニングに利用する動画を選択する。Copy videos to project folder にチェックをいれておく。Browse folderrs をクリックして、動画のあるフォルダーを指定すると(動画そのものではない)、そのフォルダーにある動画のリストが表示される。下図のように必要な動画以外のチェックを外す。
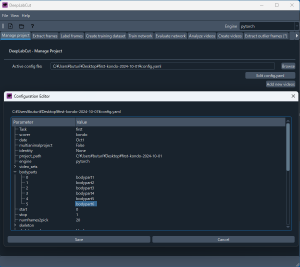
create ボタンを押して閉じる。設定をデフォルトから変更する必要があるので、Edit config.yaml をクリックする。下図のような画面が開く。最初の設定では body parts の数が足りない。下図のように bodypart を 6 個に増やす。変更する時には、ダブルクリックで項目の編集が可能となり、また枝を右クリックすると、新たに項目を追加することができる。
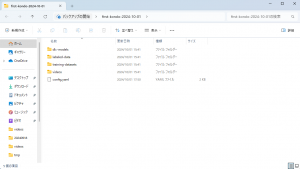
save ボタンを押して窓を閉じる。デスクトップに下図のような中身のフォルダーが作成されていることを確認する。
config.yaml には先ほどの設定が書き込まれている。videos フォルダーには、選択した動画がコピーされている。
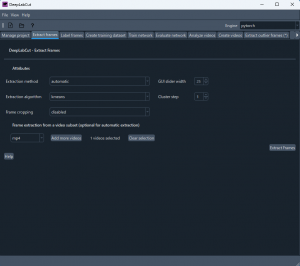
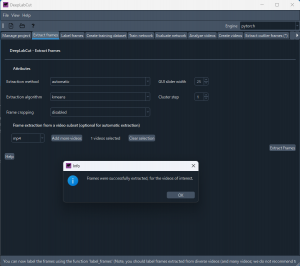
Extract frames タブを表示する。select video ボタンで機械学習のトレーニング用動画を指定する。先ほどコピーした動画を選ぶと、1 video selected と表示される。
続いて、Extract frames ボタンをクリックする。これにより選択した動画から訓練用の静止画が抽出される。
抽出が完了すると、下図のように、labeled-data フォルダー内に 20 枚の画像が切り出されている。
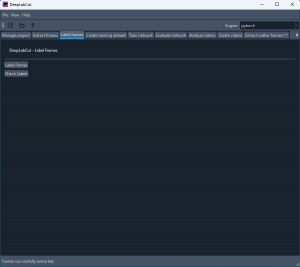
次に Label frames タブに移る。ここでは抽出した静止画に対して、トレーニング用の正解を用意する(色つきシールの位置を教える)。
Label Frames ボタンをクリックすると、フォルダーの選択が促されるので、先ほどの 20 枚の静止画があるフォルダーを指定する。その後、下図のような窓が開く(最初に表示されるチュートリアルは実施する必要はない)。以下では、窓を大きくしてパソコンのモニター画面最大サイズにした方が作業がしやすい。
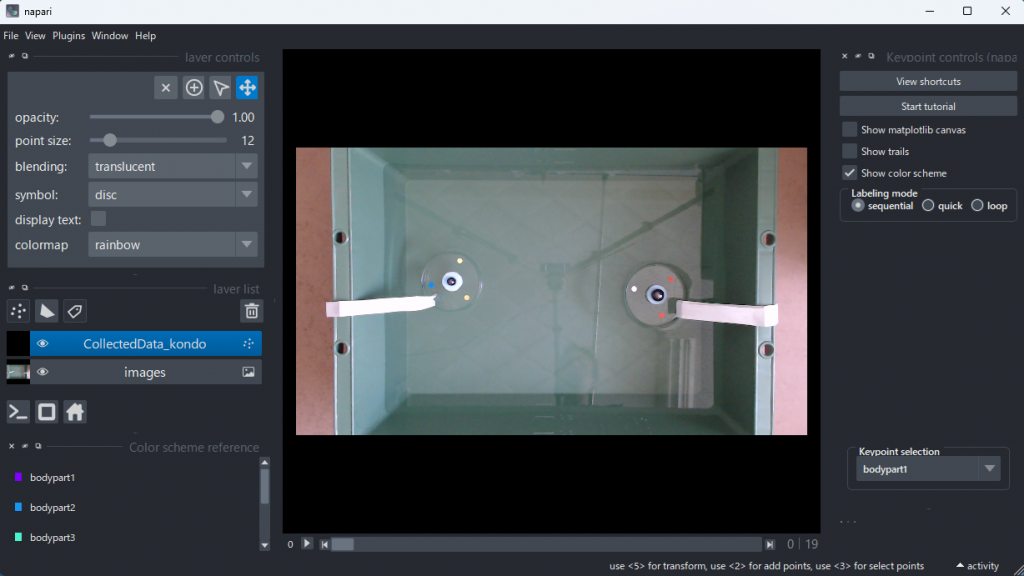
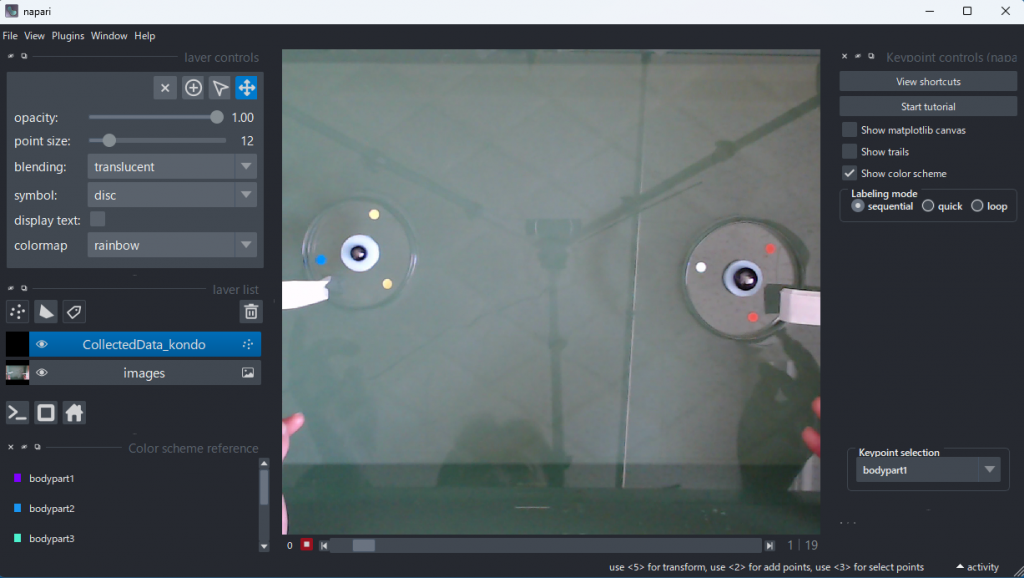
窓の下方に動画の再生制御機能が並んでいる。動画は 20 枚の静止画で構成されている。動画を再生しながら、追跡したい物体の移動範囲を確認する。以降、物体の位置にしるしをつけていくが、作業しやすいように動画の表示を拡大する。拡大にはマウスホイールを利用する。色つきシールが表示枠内に収まっていることを確認したら、動画を静止させ再生位置を1枚目の画像に戻す。
左上方にある丸にプラスマークが入ったアイコンをクリックして座標位置の指定を始める(クリックすると下図のようにアイコンが青くなる)。静止画一枚ごとに、マウスクリックで追跡する位置を指定していく。下図は1枚目の画像の作業中で、 3 ポイントしるしを付けたところである。左側の磁石を囲む 3 個のシールに印がついている。マウスをクリックすると自動的に次のポイントの指定に移る。6 ポイント印をつけたら、次の静止画像に切り替える。
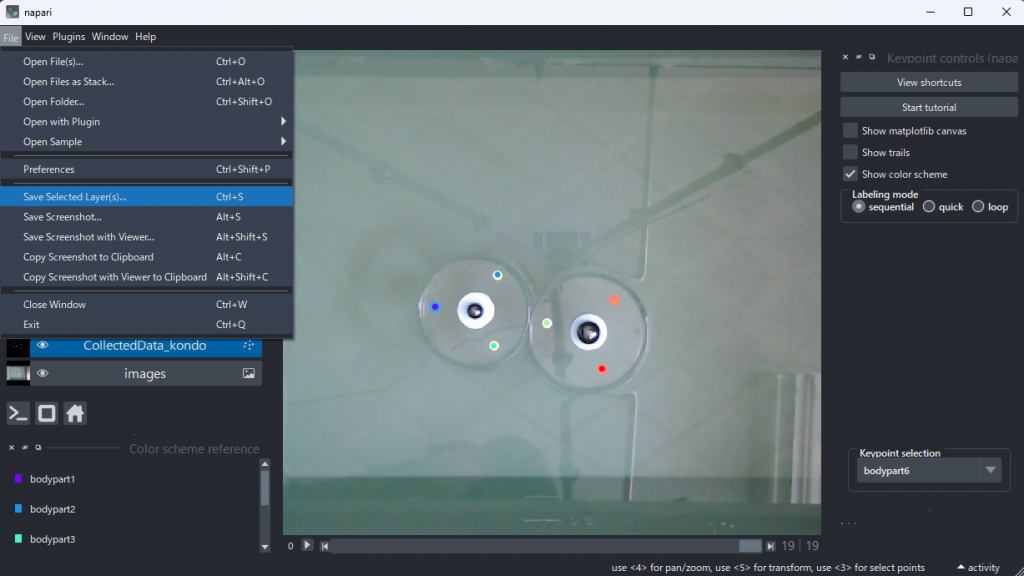
静止画 20 枚すべてに印を付けたら終了である。窓を閉じる前に作業結果を記録する(重要)。下図のようにメニューバーから File を選び、Save Selected Layer(s) を実行する。記録したら窓を閉じる。
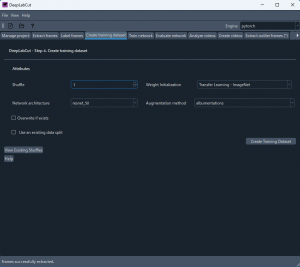
Create training dataset タブに切り替える。ここでは何も変更せず、Create training dataset ボタンをクリックする。
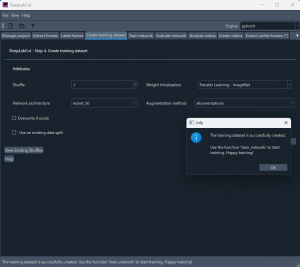
データセットが作成された。
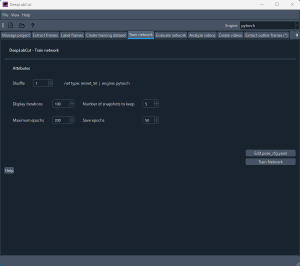
続いて、Train network タブに移る。ここでは Display iterations を 100 に変更する。その後、Train Network ボタンをクリックして訓練を開始する。
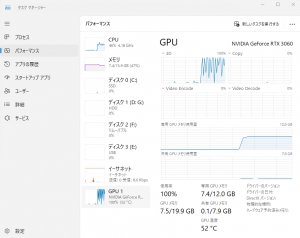
タスクマネージャーを開くと、gpu のメモリ使用量が急上昇しているのが確認できる。これはトレーニングに GPU の演算機能を利用していることを示している。
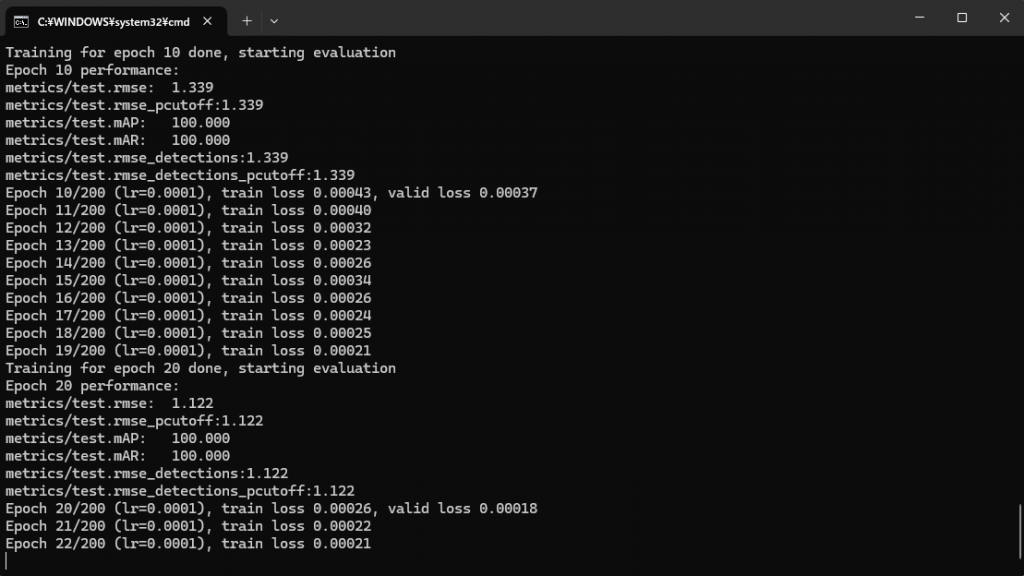
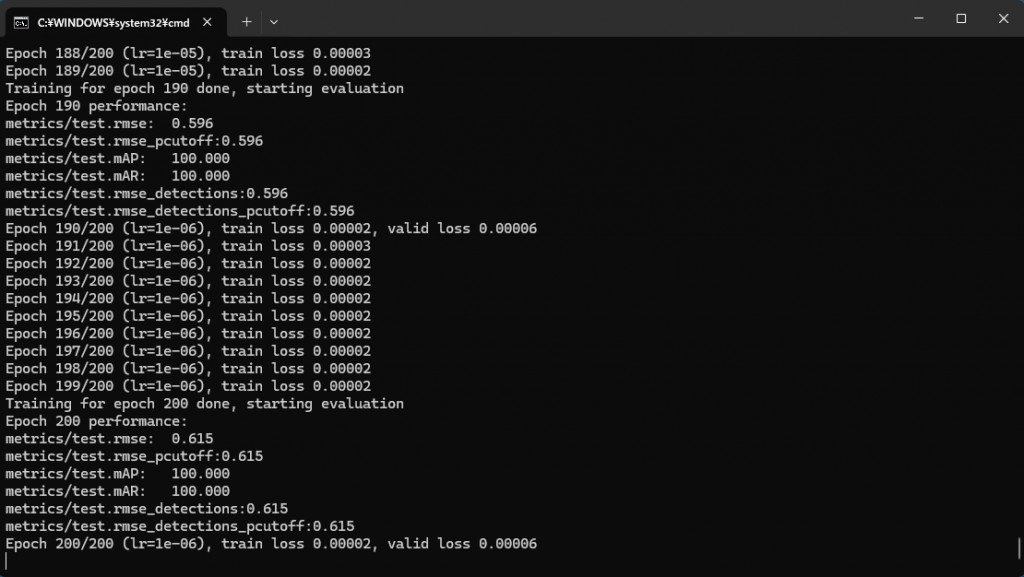
途中経過は、 deeplabcut を起動した端末に表示される。端末には、この他の作業中にもメッセージが表示される。
25 分程度でトレーニングは終了する。
端末の表示を見ると、この訓練では、後半はもはや train loss は減少していない。
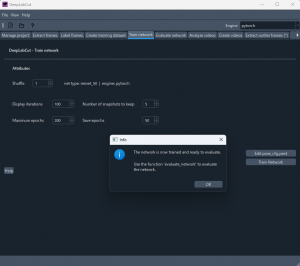
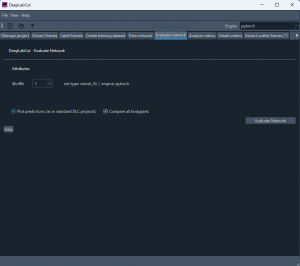
Evalute network タブに移る。Evalute network ボタンをクリックする。
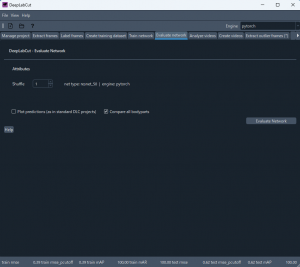
下図のように、窓の下の辺にメッセージが表示される。
ここでプロジェクトを保存しよう。次の Analyze videos タブでの作業において、30 分以上の時間がかかってしまうトラブルが、これまで何回か生じている。その原因は不明であるが、 deeplabcut をいったん終了し再び起動した後、作業をこの位置から再開すると、そのトラブルを回避して通常の時間(2,3 分間)で解析が終了した。そのためここでプロジェクトを保存しておく方が賢明である。
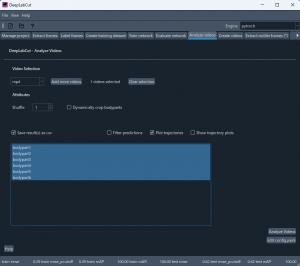
Analyze videos タブに移る。手順通りであれば、すでに 解析するビデオが選ばれている。他のビデオを解析する時には、ビデオの選択をやり直す。トレーニング結果は他の動画にも利用できるので、他の動画を解析する際にトレーニングをやり直す必要はない。ここで他の動画を選択するだけで良い。
Save result(s) と Plot trajectories にチェックを入れて(下図ではすべての bodypart を選んでいる)、Analyzed videos ボタンをクリックする。
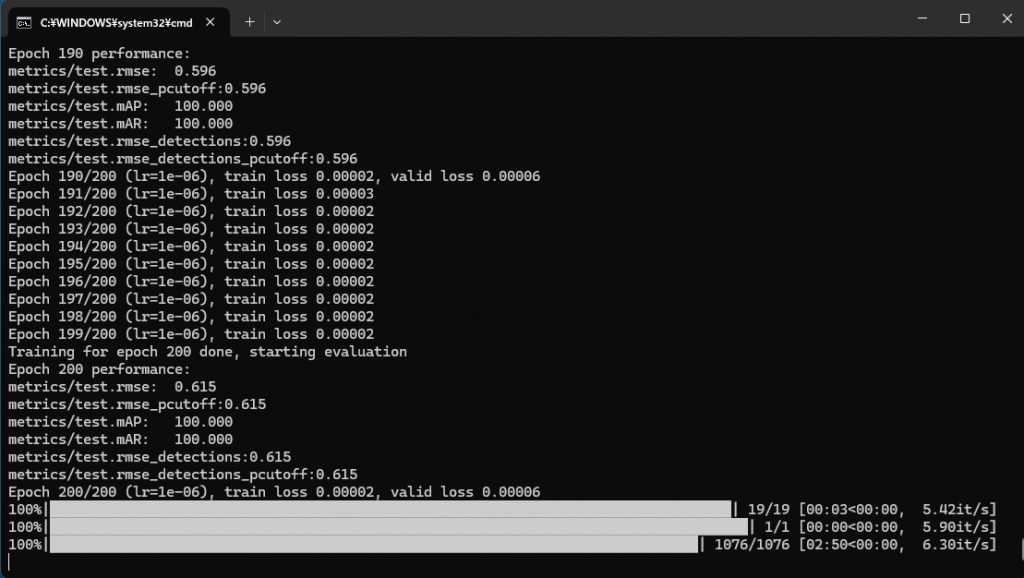
解析には 2, 3 分を要する。この時も下図のように端末に途中経過等が表示される。下図では 2 分 50 秒ほどかかっている。
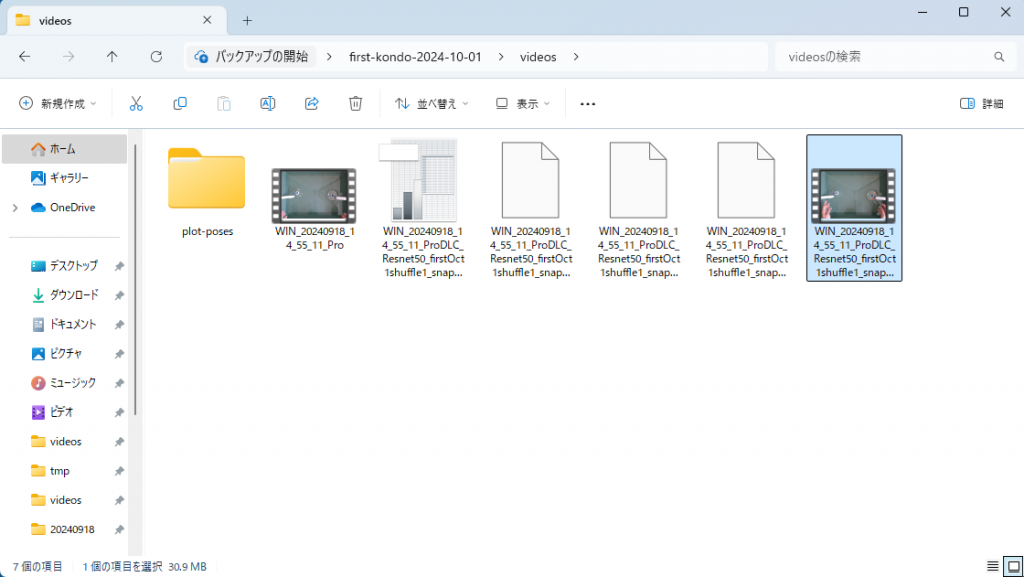
解析が終了すると、videos フォルダーには読み取った座標値を記した csv ファイルが現れる。
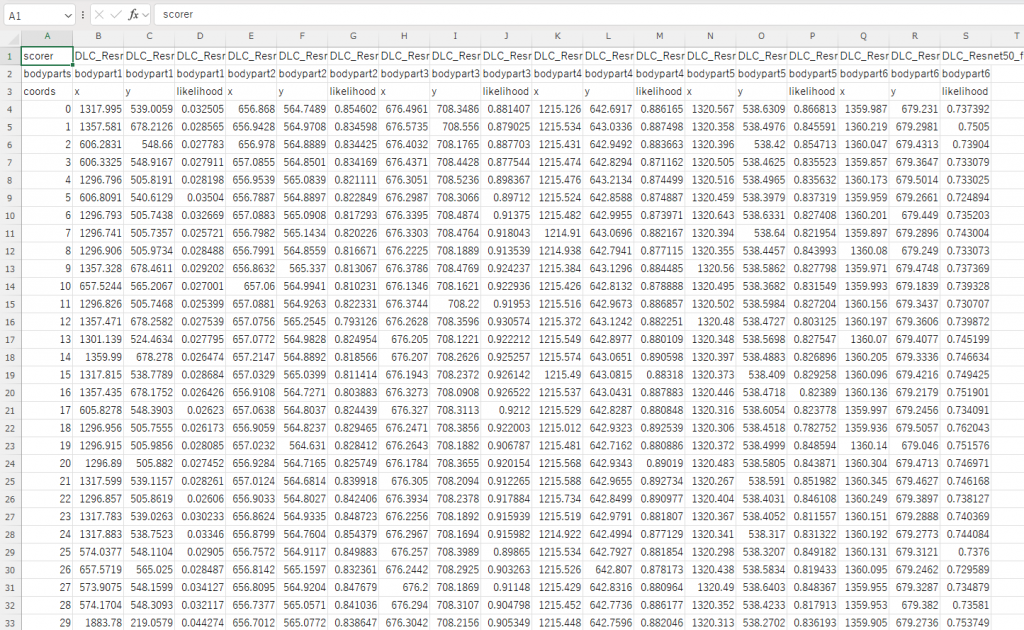
csv ファイルは下記のような内容である。全ての bodyparts の、ピクセル座標が記録されている。
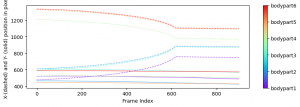
videos/plotposes フォルダーの中にその動画専用のフォルダーが作成されて、その中には位置座標の時間変化のグラフや軌跡の図が作成される。下図は位置座標の時間変化のグラフの例である。
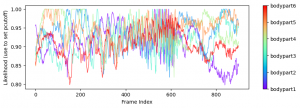
下図は、座標の読み取りにどれぐらい自信があるかを示す plot-likelihood のグラフの例である。
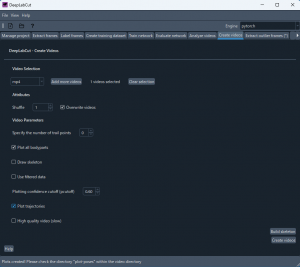
Create videos タブに移る。ここでは解析した結果を元の動画に上書きした映像を作成する。手順通りであれば、すでに対象となる video が選択されている。下図のように Overwrite videos と Plot trajectories にチェックを入れて、Create videos ボタンをクリックする。
読み取った位置を示すマークが上書きされた動画が作成され、下図のように videos フォルダーに新しい動画が現れる。なぜか上書きが上手くいかないことがあって元の動画のままの場合があるが、その時は作成された動画をいったん削除して、もう一度 Create videos ボタンをクリックすると良い。
読み取った位置が上書きされた動画の例を下に示す。
色付きシールのあたりの色が変わって少し大きめの丸になっている。色つきのシールの位置を上手く追跡できていることが確認されたので、機械学習のトレーニングが的確であると分かった。このトレーニング結果は、他の動画ファイルの解析にも利用できる。トレーニングには必ずしも良い測定動画を用いる必要はない。トレーニングでは磁石周辺の外見的特徴を学ぶだけで良いので、極端に言えばどのような運動をしている動画でも両方の磁石が写っていれば利用可能である。
4.4 解析
マークを上書きした動画を報告用のパワーポイントファイルに張り付ける(下図)。また、はかりでシャーレを含めた船全体の質量を測定し、これも報告用のファイルに記入する。ここでは、左側の磁石のセットが 58.7 g、右の磁石の方が 78.6 g である。
以下の解析では、ピクセル座標 (Px, Py) と実座標 (x, y) の換算式は下記を用いている。各自班ごとに定めた換算式を利用すること。
- x = -36.96+0.03963*Px-0.0003398*Py+6.089*10^(-7)*Px^2+1.529*10^(-8)*Py^2
- y = 23.70-0.0003167*Px-0.04060*Py-1.335*10^(-8)*Px^2-2.149*10^(-7)*Py^2
以下、座標位置を検出した CSV ファイルの解析を進める。下記に解析を実施した後のエクセルファイルをあげるので、参考にしてください。
動画を解析すると、下図のような 6 セットのピクセル座標の組(Px, Py の組)が記述された CSV ファイルが得られる。CSV ファイルを読み込んだら、解析を進める前にエクセルファイルとして保存する。CSV ファイルのままでは、グラフや解析結果が保存されないので必ずエクセルファイルへ変換すること。 シートの値から、二つの磁石の位置に対応する二組の(Px, Py)を求める。これ以降、左側の磁石を A、右側の磁石を B と呼称する。色つきシール 3 点のピクセル座標を平均して、ひとつのピクセル座標(見出しは Ax, Ay)を計算し、その後その値を実座標(見出しは 実x座標、 実y座標)に換算する。撮影の多くは一コマ 1/30 秒であるが、1/15 秒の時もあり、動画のプロパティーをみて確認する。下図では 1/30 秒であり、表に時間軸(見出しは time)を新たに加えている。必要ない時刻のデータは削除して構わない。
磁石の座標が得られたので、まず重心の x 座標と y 座標を求める。シートの列数が増えて煩雑になるので、新たにシートを追加して、そこに時間と実座標のデータをコピーした(下図)。下図では重心の座標も求めて追加している。
磁石A、Bと重心の、 x 座標の時間依存性グラフを作成し(下図)、報告用パワーポイントファイルに張り付ける。
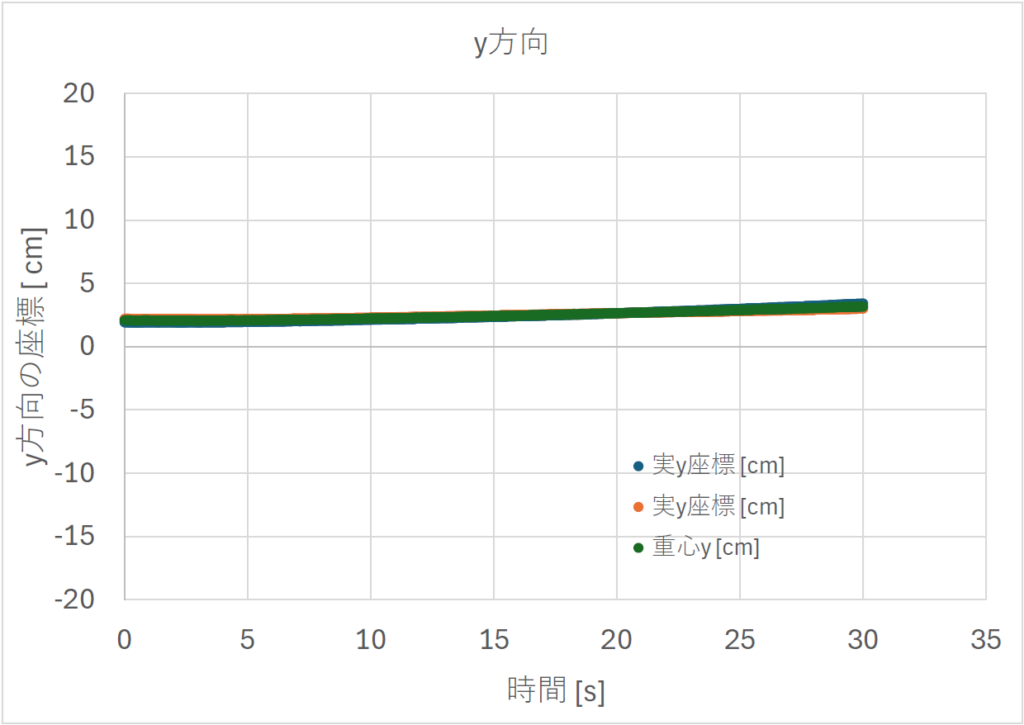
同様に、磁石A、Bと重心の、 y 座標の時間依存性グラフを作成し(下図)、報告用パワーポイントファイルに張り付ける。グラフの縦軸を x 座標のグラフと合わせると大きさの比較がしやすい。
上図のグラフでは、重心が多少移動している。移動すること自体はあり得ることであるが、その速度が変化している場合は何かの外力が働いていることを示す。
続いて運動量を検討する。新しくシートを追加した(下図)。下図では、それぞれの磁石の速度と運動量を求めている。
速度は slope 関数を利用して求める。slope 関数とは、上図のように領域を定めて(A2からB6まで)平均的な傾きを求めるものである。D4セルの値を 5 ポイントの測定結果から求める場合、下記のように記述する。
- =SLOPE(B2:B6,$A2:$A6)
求めた速度に質量をかけて運動量を算出する。また A と B の運動量の和の列も作成する。
最初に A と B の運動量の x 成分のグラフを作成する(報告ファイルに追加)。下図の緑の点は両磁石の運動量の和である。和は一定の値となっている。
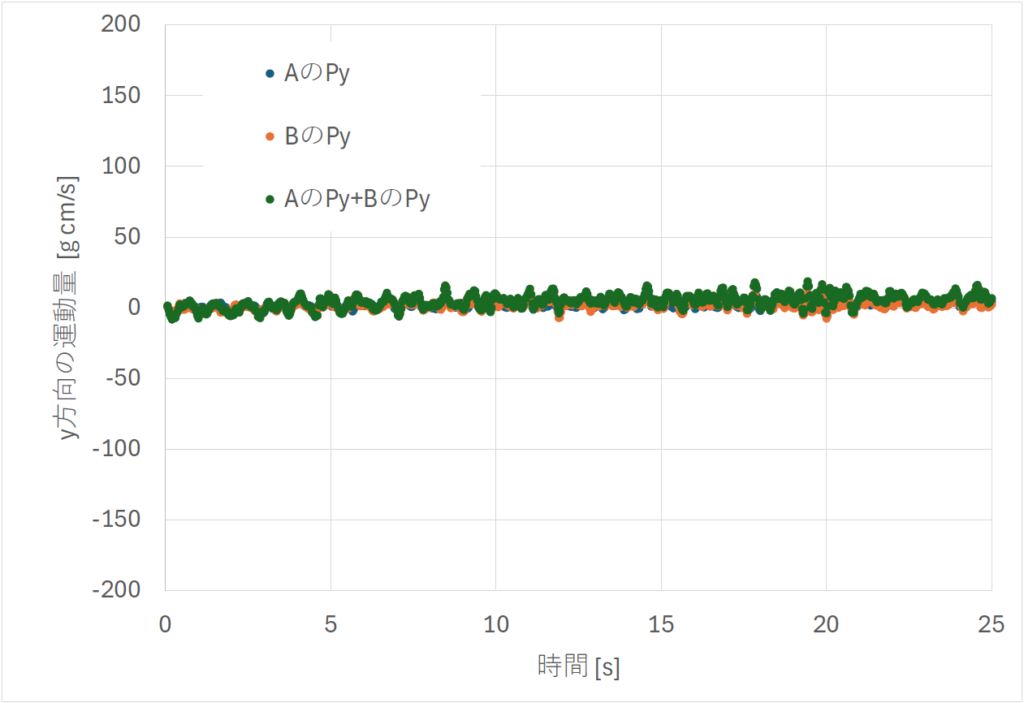
次に、y 方向の運動量のグラフを作成する(報告ファイルに追加)。
グラフの縦軸を x 成分と合わせている。両成分とも変化が見られない。和の値にも大きな変動はない。
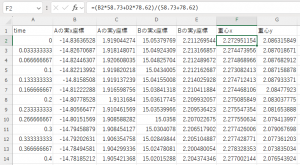
最後に、それぞれの磁石の加速度から力を求める。シートを追加する(下図)。加速度は先の速度の計算結果から求めるのではなく、座標の値にいったん立ち返り、座標を時間の2次式でフィットし、その係数から加速度を求める。その計算には LINEST 関数を使用する。2次でフィットするために、時間を2乗した列も用意する。速度とは異なり、約 2 秒ぐらいの長い時間間隔の測定データを用いて近似する。
例えば、x 座標を下記のような時間の2次式でフィットする。
- x = a*time^2 + b*time + c
その時間の2次の係数 a の2倍が加速度となる。 LINEST 関数は係数を配列として返す。その配列の インデックス 1 が2次の係数である。計算には、前後約1秒間のデータを利用する。下記に計算例をひとつ上げる。セル E31 の計算の場合である。
- =INDEX(LINEST(C2:C60,$A2:$B60),1)*2
これによって求めた加速度に質量をかけて力とし、グラフを作成する(報告ファイルに追加)。下図は力の x 成分のグラフであるが、磁石 B の方の符号を反転させている。
波打っているところは、水面の波が影響しているのかもしれない。力が大きいところでは良い一致を示している。
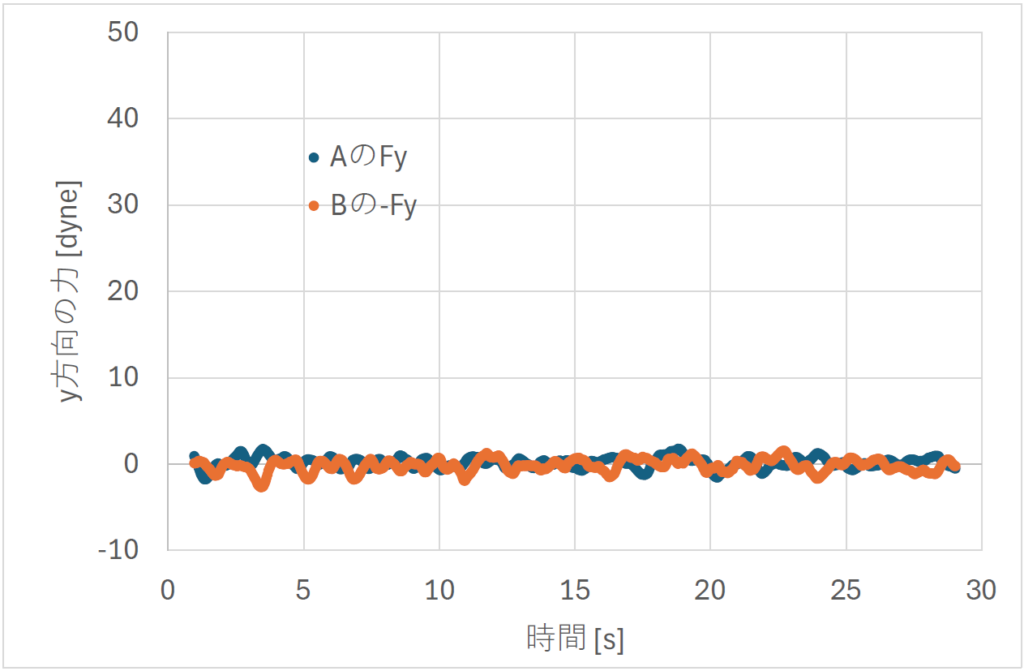
力の y 成分のグラフを作成する(報告ファイルに追加)。
グラフは x 成分と同じ縦軸を採用した。y 成分は x 成分と比較して全般的に小さな値である。両成分とも 約 2 秒間の平均であるから、衝突の影響は衝突時刻よりも 約 1 秒早く現れることに注意する。
以上で、実験は終了です。報告用のパワーポイントファイルを TA に点検してもらった後、提出してください。そのあとで、アンケートにご協力ください。Moodle にあるアンケート(匿名です)と紙で回答するもの(これも匿名)の二つをお願いします。